Kunci Jawaban Eksplorasi Matematika halaman 204 Misteri Luas Daerah Matematika SMP Kelas 8 Kurikulum Merdeka
kontenjempolan.id-Kunci Jawaban Eksplorasi Matematika halaman 204 Misteri Luas Daerah Matematika SMP Kelas 8 Kurikulum Merdeka.
Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 204. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Matematika Lanjut.
Eksplorasi Matematika
Misteri Luas Daerah
1. Tentukan luas daerah A dan B pada grid atau persegi kecil di sebelah kanan.
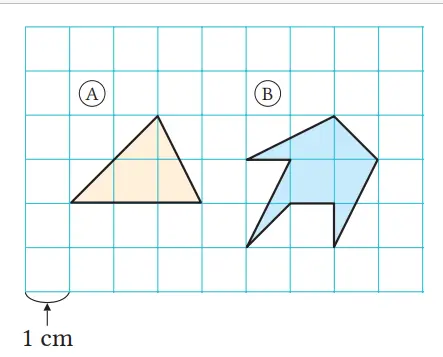
Untuk menentukan luas daerah pada sebuah grid, untuk kasus A , luas daerah mudah ditentukan, tetapi untuk kasus B , luas daerah sulit ditentukan.
Pada sebuah grid, titik perpotongan antara garis vertikal dan horizontal dinamakan titik latis. Perhatikan titik-titik latis pada bagian dalam dan pada gambar, lalu selidikilah luas daerahnya.
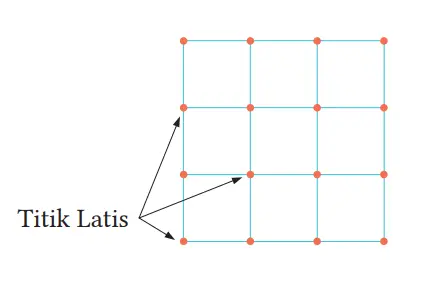
Jawaban:
Ⓐ 3 cm2
Ⓑ 4 cm2
2. Bangun datar dengan satu titik latis di bagian dalam.
(1) Tentukan banyaknya titik latis pada gambar a ~ e , tentukan luas daerahnya, dan tuliskan hasilnya dalam tabel di bawah.
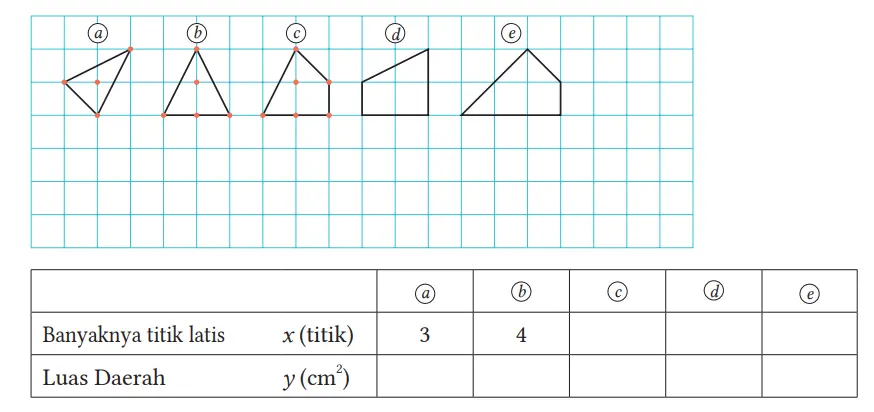
Jawaban:
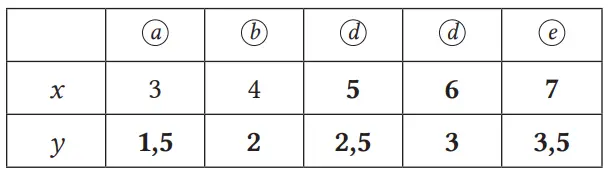
(2) Jika kita misalkan luas daerah dengan y ketika banyaknya titik latis pada gambar adalah x, maka nyatakan y dalam x.
Penjelasan dan Hal yang Perlu Diperhatikan
1. Teorema Pick
Sifat bangun datar yang kita pelajari di sini disebut “Teorema Pick”. Artinya, jika jumlah titik latis pada keliling gambar yang dibentuk dengan menghubungkan titik latis adalah x, luasnya y, dan jumlah titik latis di dalamnya adalah n, maka hubungannya menjadi
y = 1/2x + n – 1
Berharap peserta didik merasa terkejut dapat mengetahui luas bidang dari jumlah titik latis.
2. Pengerjaan 1
Mencari luas gambar dengan metode biasa.
(A) dapat kita peroleh langsung dengan menggunakan rumus luas segitiga, tetapi (B)membutuhkan beberapa keterampilan seperti membagi atau memindahkan bangun. Kami fokus pada hubungan antara jumlah titik latis dan luasnya, sebagai metode untuk menemukan luas dengan mudah, bahkan dengan gambar seperti itu.
3. Pengerjaan 2
Jumlah titik latis bagian dalam ditetapkan, dan hanya jumlah titik latis pada keliling yang diubah untuk menyelidiki bagaimana luas permukaan berubah.
Menggunakan batas grid, saya ingin menggambar figur selain a – e , dan memeriksanya dengan cara yang sama. Misalnya, sebuah gambar dengan empat titik latis pada kelilingnya dapat digambar seperti ini, yang mana pun luasnya 2 cm2.
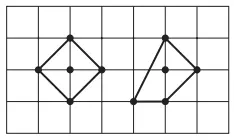
3. Bangun datar dengan dua titik latis di dalam.
(1) Carilah banyaknya titik latis pada gambar f ~ i , tentukan luas daerahnya, dan tuliskan hasilnya pada tabel di bawah.
(2) Buat dua gambar dengan dua titik latis di bagian dalam h dan i , dan selidiki dengan cara yang sama.
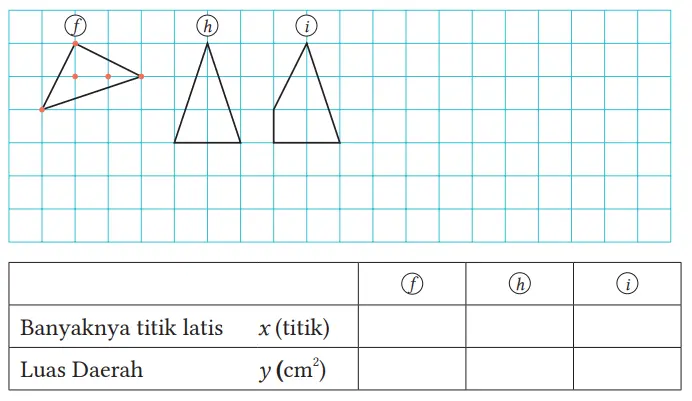
(3) Nyatakan y dalam x.
Jawaban:
(1) (2)
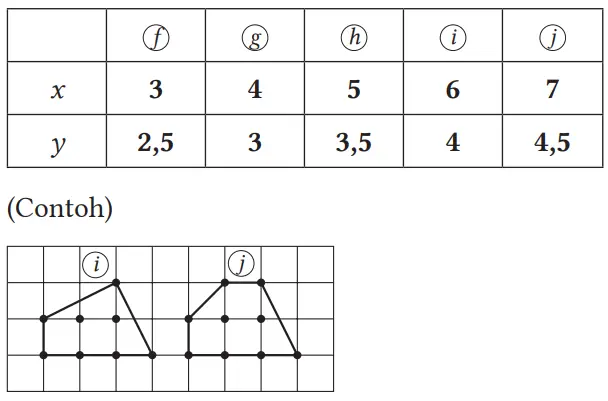
(3) y = 1/2x + 1
4. Bangun datar dengan tiga titik latis di bagian dalam. Selidiki dengan cara yang sama seperti dalam 3 dan nyatakan y dalam x.
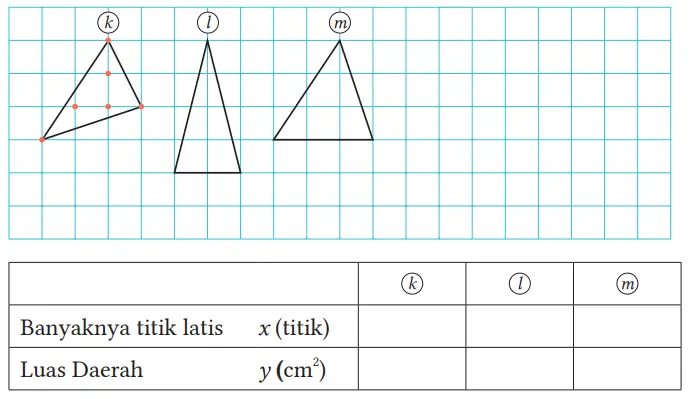
Jawaban:
(1) (2)
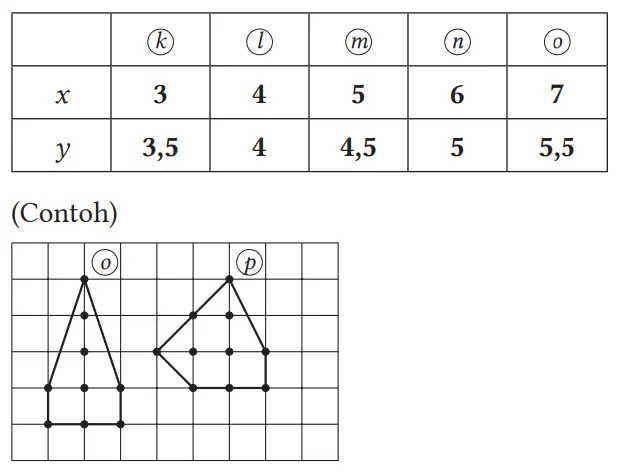
(3) y = 1/2x + 2
Pengerjaan 3 , 4
Poin j dan k pada gambar 2 adalah contoh. Karena jumlah titik latis bagian dalam hanya dua, berbagai gambar lain dapat kita gambar. Sambil menunjukkan bangun datar yang peserta didik pikirkan, saya ingin memastikan bahwa jika jumlah titik latis pada kelilingnya sama, luasnya akan sama.
y = 1/2x + 1
Selain itu, jika membandingkan tabel yang dibuat dengan 3 dan 2, ditemukan bahwa nilai y selalu lebih besar 1 untuk nilai x yang sama, sehingga mengarah pada rumus. 4 juga diperlakukan sama.
5. Bangun datar tanpa titik latis di dalam.
Selidiki dengan cara yang sama seperti pada 3 dan 4 di halaman sebelumnya, dan nyatakan y dalam x.
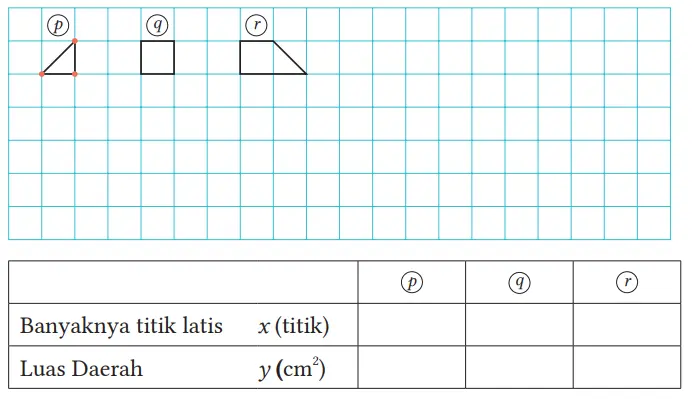
Jawaban:
(1) (2)
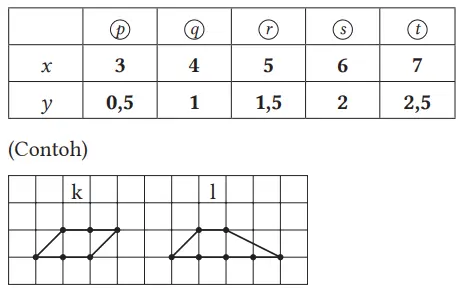
(3) y = 1/2x – 1
6. Rangkumlah hasil-hasil sebelumnya ke dalam sebuah tabel dan buat dugaan hubungan antara x dan y ketika banyaknya titik-titik latis dalam gambar meningkat menjadi 4, 5, …. Selain itu, misalkan banyaknya titik latis adalah n, dan nyatakan y dalam x dan n.
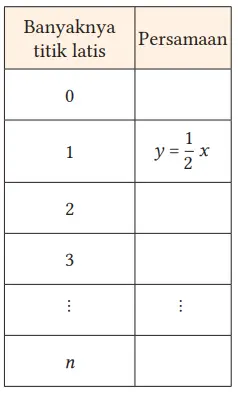
Jawaban:

Jika jumlah titik latis bagian 4, 5, … ditingkatkan, masing-masing diperkirakan menjadi
y = 1/2x + 3, y = 1/2x + 4, …
Dengan kata lain, y = 1/2x + (jumlah titik latis bagian dalam) – 2
Jika kita ringkas persamaan yang kita buat sejauh ini dalam tabel, dapat kita lihat bahwa ketika jumlah titik latis bagian dalam bertambah, hanya bagian konstanta yang bertambah satu. Jika prediksi kasus di mana jumlah titik latis internal adalah 4, 5, …, 10, dan seterusnya, maka secara umum mengarah pada rumus
y = 1/2x + n – 1
7. Periksa apakah bentuk aljabar yang diperoleh pada bagian 6 berlaku dengan cara membuat berbagai bentuk gambar bangun datar.
Jawaban:
(Contoh)
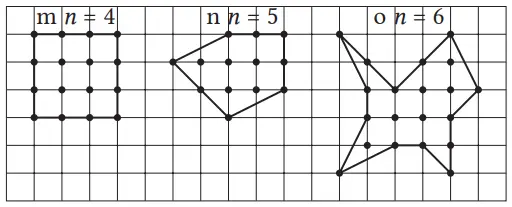
Bangun datar… luasnya 12.
n = 6, x = 14 y = 1/2x + n – 1
y = 1/2×+ 14 + 6 – 1 = 12
Dengan demikian, rumusnya tepat (bangun datar, sama).
Pengerjaan 7
Mencari nilai n, x, dan y dari gambar yang oleh peserta didik sendiri gambar, dan memastikan apakah rumus di atas berlaku.
Disclaimer:
Kunci Jawaban pada unggahan kontenjempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
Demikian pembahasan Matematika Kelas 8 Eksplorasi Matematika halaman 204 Misteri Luas Daerah. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.



