Persamaan I dan Persamaan II Halaman 211 Grafik Persamaan Garis Lurus Matematika SMP Kelas 8 Kurikulum Merdeka
kontenjempolan.id-Persamaan I dan Persamaan II Halaman 211 Grafik Persamaan Garis Lurus Matematika SMP Kelas 8 Kurikulum Merdeka.
Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 211. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Persamaan Garis Lurus.
Persamaan Garis Lurus
Graik Persamaan Garis Lurus

Suatu Perusahaan diizinkan untuk mengurangi nilai aset mereka. Depresiasi garis lurus adalah istilah akuntansi untuk praktik ini. Masa pakai aset ditentukan melalui pendekatan ini. Setelah itu, aset tersebut disusutkan setiap tahunnya dengan jumlah yang sama sampai nilai kena pajaknya nol. CV. Spirit 45 menghabiskan Rp360.000.000,00 untuk sebuah truk baru. Nilai truk akan turun Rp12.000.000,00 setiap tahun. Harga kendaraan dinyatakan dalam persamaan penyusutan y= 360.000.000 – 12.000.000x, dengan x adalah umur truk dalam tahun.
Bagaimana cara kalain dapat mencari letak perpotongan garis dengan sumbu-x dan sumbu-y? Bagaimana persamaan yang menggambarkan depresiasi harga kendaraan dapat digambarkan pada bidang koordinat?
Sekarang, untuk menjawab dua pertanyaan berikutnya dengan benar, coba perhatikan baik-baik bagaimana garis-garis lurus tertentu pada koordinat Cartesius berikut ini digambarkan.
Persamaan I
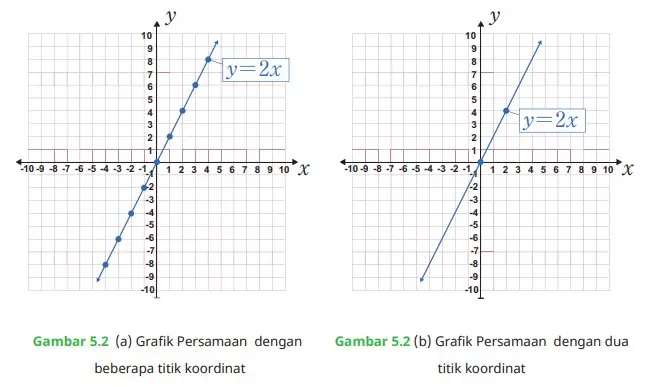
Berdasarkan Gambar 5.2 (a), lengkapi sel tabel berikut ini.
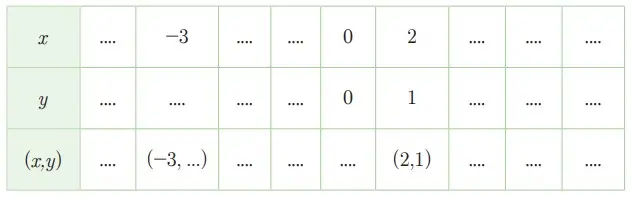
Selanjutnya berdasarkan Gambar 5.2(b), lengkapi juga sel kosong pada tabel berikut.
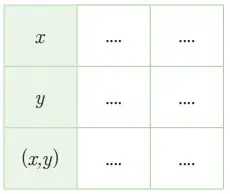
Persamaan II
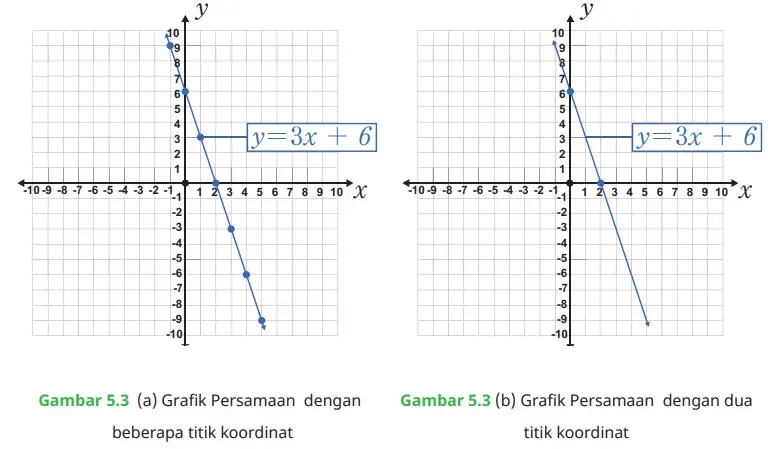
Berdasarkan Gambar 5.3 (a), lengkapi sel tabel berikut ini.

Selanjutnya berdasarkan Gambar 5.3 (b), lengkapi juga sel tabel berikut ini.
Berdasarkan hasil kegiatan pada kedua persamaan di atas, coba kalian eksplorasikan hasil diskusinya dengan menjawab dua pertanyaan berikut ini.
1. Syaratnya apa sajakah suatu persamaan graik bisa membentuk suatu garis lurus?
2. Adakah rumus persamaan garis lurus yang secara tepat memotong sumbu-x dan sumbu-y pada satu titik?
Definisi
Persamaan y = 3x + 2 dapat dinyatakan dalam bentuk umumnya sebagai y = mx + c , di mana x dan y adalah variabel, c adalah konstanta, dan m adalah kemiringan atau koeisien arah.
Tahukah Kalian?
Matematikawan Rene Descartes berasal dari Prancis. Dia adalah orang pertama yang menyarankan bagaimana mengekspresikan suatu titik sebagai sepasang bilangan bulat yang menunjukkan seberapa jauh dari masing-masing sumbunya. Nama sistem notasi titik seperti ini disebut dengan koordinat Cartesius.
Contoh 5.1
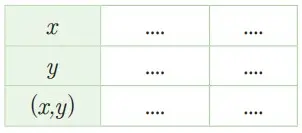
Lengkapi sisa sel yang kosong pada tabel berikut dan gambarkan graiknya dari persamaan 4x – y = 5.
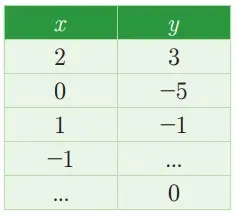
Alternatif penyelesaian
Untuk x = -1, terdapat 4x – y = 5
4(-1) – y = 5 substitusi nilai x = 1
-4 – y = 5 sederhanakan
– y = 9 jumlahkan kedua ruas oleh 4
4y = 9 kalikan kedua ruas oleh -1
Untuk y = 0, terdapat 4x – y = 5
4x – 0 = 5 substitusi y = 1
4x = 5 sederhanakan
x = 5/4 bagi kedua ruas oleh 4
Tabel setelah dilengkapi sebagai berikut:
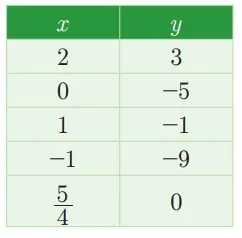
Berdasarkan tabel di atas, menunjukkan bahwa pasangan berurutannya adalah (2,3), (0,-5),(1,-1),(-1,-9), dan (5/4,0). Himpunan pasangan berurutan dibentuk oleh titik-titik dalam koordinat Cartesius yang membentuk garis lurus. Persamaan 4x – y = 5 memiliki penyelesaian pada setiap pasangan berurutan.
Garis lurus akan terbentuk jika titik-titik selesaiannya dihubungkan. Berikut ini adalah cara menggambar garis melalui titik-titik.
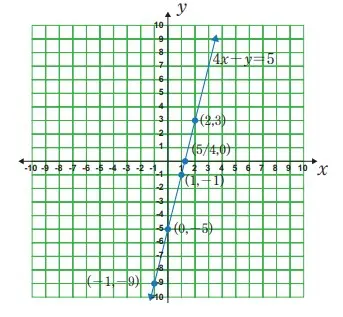
Gambar 5.4 Graik persamaan garis lurus 4x – y = 5
Persamaan 4x – y = 5 memiliki semua solusi yang terwakili oleh garis lurus tersebut. Persamaan memiliki solusi di setiap titik di sepanjang garis.
Contoh 5.2
Dengan menentukan titik perpotongan pada sumbu-x dan sumbu-y, gambarkan grafiknya dari persamaan y = -1/2x – 1.
Alternatif penyelesaian
Temukan titik potong masing-masing sumbunya untuk memulai. Menentukan titik potong pada sumbu-x, yang berarti y = 0 .
y = -1/2x – 1
0 = -1/2x – 1 substitusi y = 0
1 = -1/2x tambahkan kedua ruas oleh 1
-2= x kalikan kedua ruas oleh -2
Sehingga, titik potong pada sumbu-x adalah ( , – 2 0).
Persamaan y = -1/2x – 1 membentuk garis lurus jika dua titik dihubungkan, seperti yang ditunjukkan pada diagram berikut.
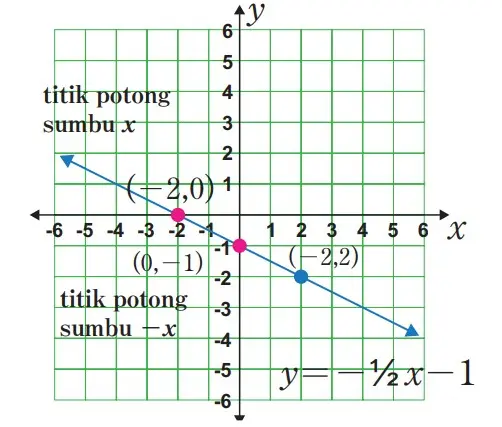
Gambar 5.5 Graik persamaan garis lurus y = -1/2x – 1
Ayo Berkomunikasi
Berdasarkan contoh 5.1 dan 5.2 tersebut, coba nalarkan pikiran kalian dengan menjawab pertanyaan berikut.
a. Contoh soal mana yang lebih sederhana dan mudah dipahami untuk diselesaikan dalam hal menggambar persamaan garis lurus?
b. Apakah mungkin menggambar garis lurus dengan menentukan dua titik saja pada bidang koordinat, atau perlukah diketahui titik-titik lain pada bidang koordinat?
c. Adakah suatu garis lurus yang hanya melalui salah satu sumbu koordinat? Jika iya ada, seperti apa persamaannya?
Tahukah Kalian?
Pengacara dan penggemar matematika dari Prancis adalah Pierre de Fermat. Dia adalah orang pertama yang menyatakan bahwa ketika diplot sepanjang sumbu-x dan sumbu-y, persamaan dapat dianggap sebagai bentuk. Asal mula grafik yang berlambangkan dengan huruf O adalah pada titik (0, 0) yang merupakan perpotongan pada sumbu-sumbu tersebut.
Ayo Mencoba
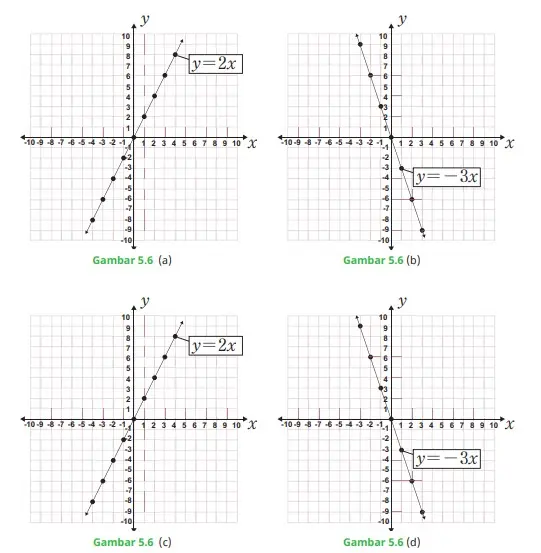
Cobalah untuk secara hati-hati dan akurat menjawab dan mendiskusikan pertanyaan berikut, sehingga kalian harus memperhatikan dengan cermat pada Gambar 5.6 di halaman berikut:
1. Apa perbedaan antara Gambar 5.6 (a), Gambar 5.6 (b), Gambar 5.6 (c), dan Gambar 5.6 (d)? Jelaskan.
2. Apa kesamaan dan perbedaan antara Gambar 5.6 (a) dan Gambar 5.6 (c)?
3. Apa kesamaan dan perbedaan antara Gambar 5.6 (b) dan Gambar 5.6 (d)?
4. Bagaimanakah perpotongan keempat garis dari keempat gambar terhadap sumbu x dan sumbu y?
Kemudian, kembali ke masalah awal penentuan tentang penurunan nilai pajak terhadap usia truk yang telah dibahas pada awal materi Bab 5 ini.
Alternatif Pemecahan Masalah
Dengan mensubstitusikan nilai y = 0, maka akan menghasilkan titik perpotongan garis dengan sumbu-x.
y = 360.000.000 – 12.000.000
0 = 360.000.000 – 12.000.000
12.000.000x = 360.000.000
x = 30
Titik potong garis dengan sumbu x adalah (30, 0)
Dengan mensubstitusikan nilai x = 0, maka akan menghasilkan titik perpotongan garis dengan sumbu-y.
y = 360.000.000 – 12.000.000(0)
y = 360.000.000
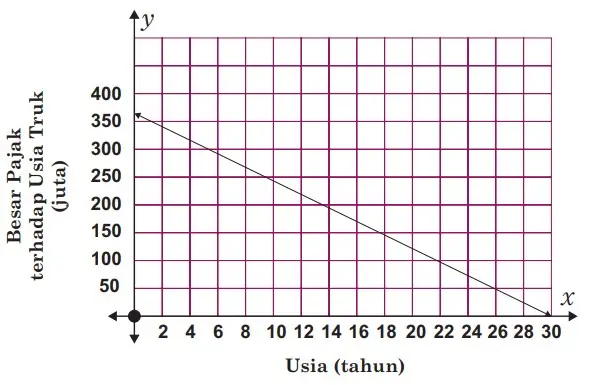
Gambar 5.7 Nilai pajak menurun seiring usia truk
Gambar 5.7 di atas menunjukkan bahwa kendaraan tersebut berharga Rp.0,00 ketika berumur 30 tahun, perpotongan garis dengan sumbu x berada di (30, 0).
Perpotongan garis yang melalui sumbu-y di titik (0,360.000.000) menunjukkan bahwa besar biaya kendaraannya adalah Rp360.000.000,00 saat masih baru (0 tahun yang lalu).
Disclaimer:
Kunci Jawaban pada unggahan kontempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
Demikian pembahasan Matematika Kelas 8 Persamaan I dan Persamaan II halaman 211 Graik Persamaan Garis Lurus. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.



