kontenjempolan.id-Kunci Jawaban Soal Laihan 5.2 Halaman 230 Pengertian Kemiringan Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 230. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Persamaan Garis Lurus.

Persamaan Garis Lurus

Pengertian Kemiringan

Soal Laihan 5.2

1. Identiikasi besar kemiringan tangga tempat tidur di bawah ini.

 

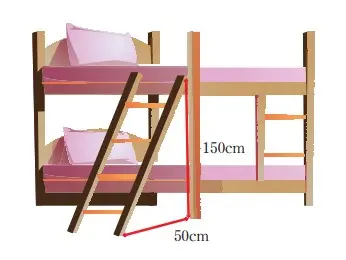
Jawaban:

Alternatif jawaban

Kemiringan tangga tempat tidur ini adalah 50/150 = 1/3

2. P dan Q mewakili dua titik pada garis untuk masing-masing graik berikut.

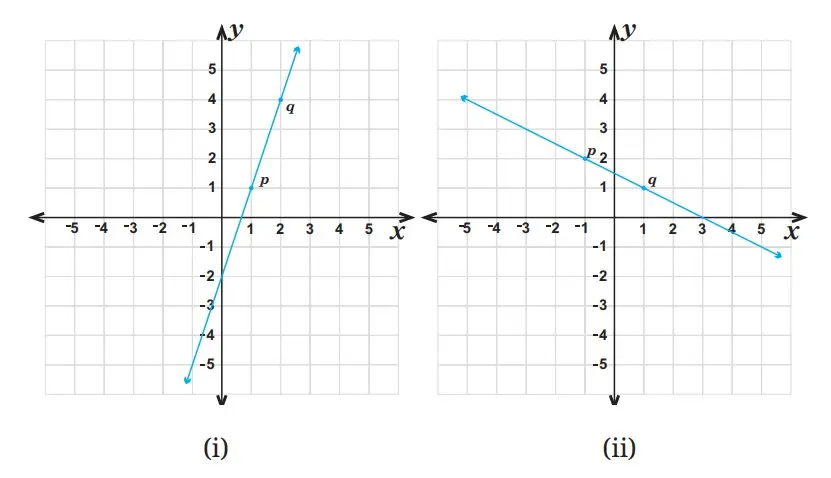
a. Berapa besar kemiringan untuk masing-masing garis tersebut?

b. Tentukan dua titik lain berbeda pada masing-masing garis tersebut, lalu hitunglah besar kemiringannya. Apakah besar kemiringan garis tersebut berubah atau tetap sama? Mengapa demikian?

Jawaban:

Alternatif jawaban

a. Kemiringan garis gambar (i) sebesar 3/1 = 3 dan garis pada gambar (ii) sebesar -1/2.

b. Karena selalu ada perbandingan antara perubahan sisi vertikal dengan perubahan sisi horizontal yang besarnya sama antara setiap dua titik pada suatu garis, maka besar kemiringan garis tetap konstan.

3. Tentukan kemiringan garis dan perpotongan pada sumbu-y untuk setiap garis lurus pada tabel di bawah ini.

Jawaban:

Alternatif jawaban

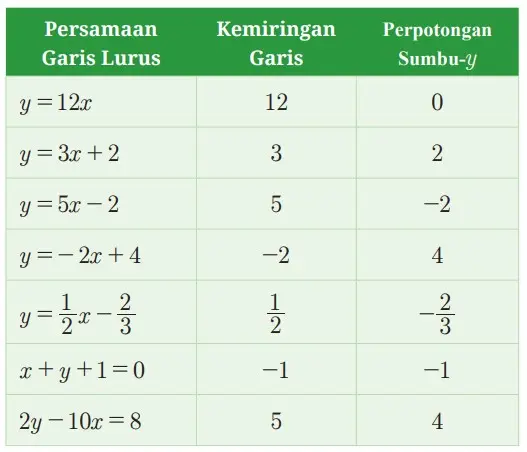
4. Asumsikan hubungan antara tinggi pesawat dan waktu terbang dalam 12 detik pertama diwakili oleh graik garis dengan kemiringan 12. Apa arti kemiringan dalam konteks ini?

Jawaban:

Artinya adalah nilai kemiringan / kecondongan suatu garis yang membandingkan antara komponen Y (ordinat) dengan komponen X (absis).

“Serahkan kepada teman Guru ”

5. Hubungan antara waktu dan volume air yang keluar dari kran terlihat pada graik di sebelah kiri. Berapa banyak kran yang harus dibuka jika kita membutuhkan 2000 liter air dalam dua jam?

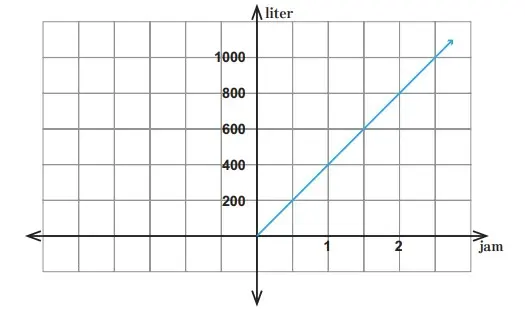
Jawaban:

“Serahkan kepada teman Guru ”

6. Apabila kemiringan garis yang melalui titik (-5,2p) dan (-1,p) besarnya sama dengan kemiringan garis yang melalui titik (1,2) dan (3,1); maka hitung nilai p.

Jawaban:

Alternatif Jawaban

Nilai p adalah 2

7. Tentukan nilai yang belum diketahui dari dua pertanyaan berikut

a. Apabila kemiringan aris yang melalui titik A (-2,3}) dan B (2,p) adalah 1/2; maka hitung nilai p.

b. Apabila kemiringan aris yang melalui titik (4,h) dan (h+3,7) adalah 1/4 ; maka hitunglah nilai h.

Jawaban:

“Serahkan kepada teman Guru ”

Ayo Berpikir Kritis

8. Apabila kalian berjalan melalui jalan yang kemiringannya besar, maka kalian akan mengalami lebih cepat capek daripada kalian berjalan melalui jalan datar. Begitu juga apabila kalian berjalan pada jalan datar dengan kemiringannya nol akan lebih cepat sampai pada tujuan daripada kalian berjalan pada lintasan yang kemiringannya lebih dari nol. Setujukah kalian dengan kedua pernyataan tersebut? Jelaskan alasan kalian.

Jawaban:

“Serahkan kepada teman Guru ”

9. Keluarga kalian mengemudi dari Cincinnati ke St Louis. Graik tersebut menghubungkan jarak kalian dari St Louis y (dalam mil) dan waktu tempuh x (dalam jam).

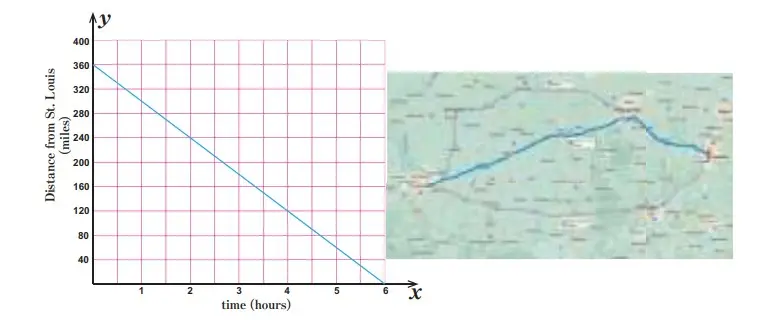
a. Interpretasikan perpotongan x dan y.

b. Apa itu kemiringan? Apa yang diwakili oleh kemiringan dalam situasi ini?

c. Tulis persamaan garis. Bagaimana graik dan persamaan berubah jika kalian dapat melakukan perjalanan dalam garis lurus?

Jawaban:

“Serahkan kepada teman Guru ”

Ayo Mencoba

10. Dalam sebuah percobaan, massa yang ditambahkan ke ujung pegas vertikal secara bertahap meningkat.

Pada akhir percobaan, komputer menghasilkan graik yang ditunjukkan di halaman berikut ini.

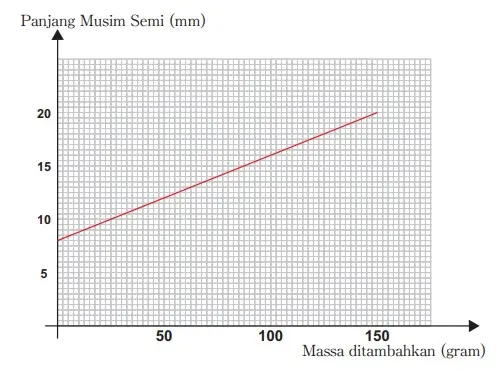
a. Tuliskan panjang pegas tanpa penambahan massa.

b. (i) Hitung kemiringan garis lurus yang ditarik pada graik.(ii) Jelaskan apa yang didapat dari kemiringan graik ini dalam kaitannya dengan eksperimen.

c. Garis lurus berhenti di depan tepi kanan kertas graik. Mengapa hal ini mungkin?

Jawaban:

Alternatif Jawaban

a. 8 cm

b. (i) 2/25; (ii) “diserahkan kepada teman Guru ”

c. “Serahkan kepada teman Guru ”

Ayo Bereksplorasi

Perhatikan bagaimana persamaan garis lurus y = mx + c dengan kemiringan m dan melalui titik ditulis (x1,y1). Setelah itu, coba fokuskan perhatian kalian pada Tabel 5.3 berikut dan selesaikan bentuk lain persamaan garis lurus dengan berbicara dengan teman-temanmu.

Tabel 5.3 Persamaan Garis Lurus dengan Kemiringan m dan Melalui Titik (x1,y1)

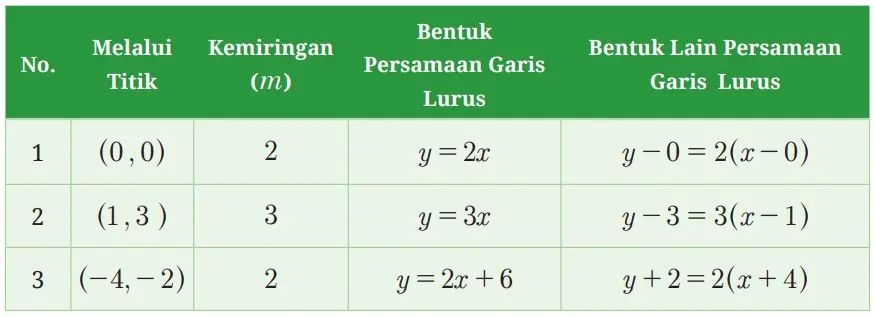
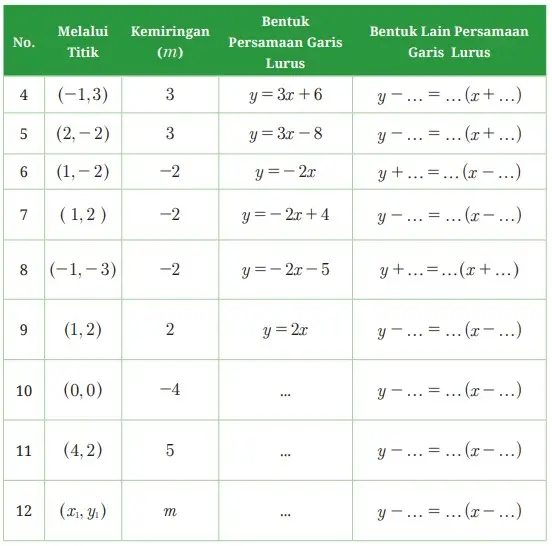
Kesimpulan apa yang dapat kalian buat dari persamaan garis lurus dan bentuk lain persamaan garis lurus yang melalui titik dengan (x1,y1) , memiliki kemiringan m berdasarkan hasil diskusimu? Uraikan hasil kesimpulan kalian.

Persamaan garis lurus yang melalui titik (x1, y1) dengan kemiringan mdapat dilihat pada Tabel 5.3 (Buku Siswa). Jadi, mintalah siswa untuk memperhatikan dengan cermat pada Tabel 5.3 tersebut. Ajaklah siswa agar memfokuskan pengamatannya pada persamaan garis lurus yang berhubungan dengan bentuk lain persamaan garis lurus, seperti y = 2x dengan y – 0 = 2(x – 0) dan bentuk umum persamaan garis lurus, seperti y = mx + c dan y – y1 = m. (x – x1).

Rumus kemiringan, m = (y2-y1)/(x1-x2); digunakan untuk menghitung kemiringan garis melalui dua titik, dan siswa diharapkan dapat memahami contoh 5.4 sampai dengan contoh 5.7 dan alternatif penyelesesaiannya.

Definisi

Persamaan garis y m= +x c merupakan suatu persamaan garis dengan gradien m dan memotong sumbu-y di titik (0, c).

Persamaan garis yang melalui titik (x1, y1), dan bergradien m adalah y – y1 = m (x – x1).

Tahukah Kalian?

Fungsi linier adalah nama lain dari persamaan garis lurus.

Contoh 5.4

Bagaimana cara mententukan kemiringan garis yang melalui titik A (2, 1) dan B (4, 5).

Alternatif penyelesaian

Misalkan (2, 1) adalah (x1, y1) dan (4,5) adalah (x2, y2). Sehingga kemiringan garis AB adalah sebagai berikut:

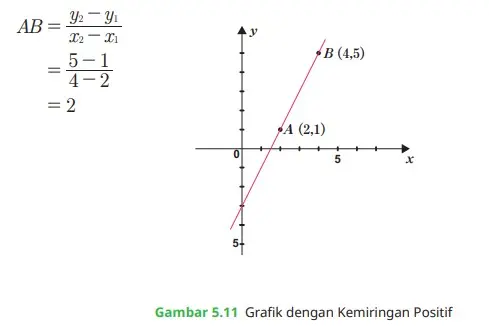
Perlu diingat bahwa apabila suatu garis memiliki kemiringan positif, maka bentuk garis tersebut selalu miring ke kanan atas.

Contoh 5.5

Tentukan kemiringan garis lurus yang melalui titik (1, 2) dan (-2, 5).

Alternatif penyelesaian

Misalkan (1, 2) adalah (x1, y1) dan (-2,5) adalah (x2, y2).

Sehingga kemiringan garis adalah sebagai berikut:

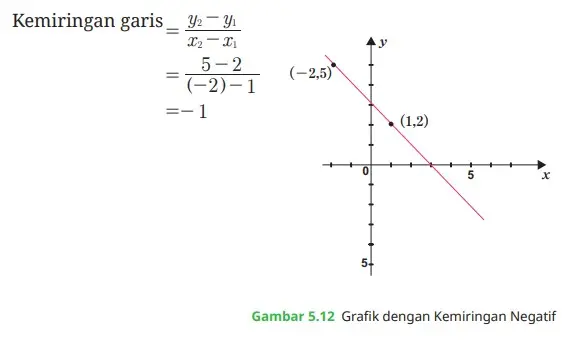
Perlu diingat bahwa apabila suatu garis memiliki kemiringan negatif, maka bentuk garis tersebut selalu miring ke kiri.

Contoh 5.6

Tentukan kemiringan garis lurus yang sejajar dengan sumbu-x dan melalui titik (1, 3).

Alternatif penyelesaian

Garis mendatar yang melalui titik (1, 3) pada graik tersebut juga melalui titik (0, 3).

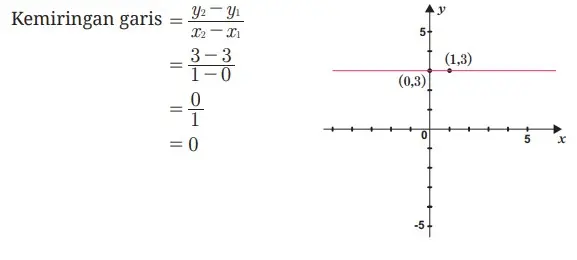
Contoh 5.7

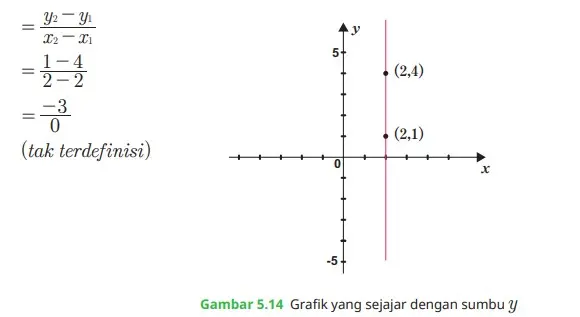
Tentukan kemiringan garis lurus yang sejajar dengan sumbu-y dan melalui titik (2, 4).

Alternatif penyelesaian

Graik vertikal melalui titik (2, 4) dan (2, 1), sehingga kemiringan garis tersebut adalah sebagai berikut.

Kemiringan garis

Ayo Berpikir Kritis

Perhatikan dengan cermat dan pertimbangkan alternatif penyelesaian dari contoh 5.4, 5.5, 5.6, dan 5.7.

1. Titik mana sajakah yang menentukan di mana suatu garis lurus melalui titik (x1, y1) dan (x2, y2) menghasilkan kemiringan positif?

2. Titik mana sajakah yang menentukan di mana suatu garis lurus melalui titik(x1, y1) dan (x2, y2) menghasilkan kemiringan negatif?

3. Apakah suatu garis tertentu dapat memiliki lebih dari satu nilaikemiringan? Jelaskan.

Berikut Alternatif Jawaban “Ayo Berikir Kritis” yang Bernilai Benar.

Apabila memungkinkan, kegiatan ini dapat terselesaikan secara mendiri oleh siswa. Adapun alternatif jawaban dari kasus ini adalah jika suatu garis lurus melalui dua titik tertentu, maka kedua titik tersebut yang dapat menentukan besar kemiringan garis yang bernilai positif atau bernilai negatif. Misalkan kedua titik tersebut adalah (x1, y1) dan (x2, y2); maka persamaan garisnya adalah (y-y1)/(y2-y1) = (x-x1)/(x2-x1); sehingga persamaan garis lurus ini hanya memiliki satu kemiringan saja.

Ayo Berpikir Kreatif

Pada kegiatan sebelumnya, kalian telah berhasil menemukan cara tertentu pada bentuk persamaan garis lurus yang melalui titik (x1, y1) dengan kemiringan m.

Oleh karena itu, coba kalian perhatikan dengan cermat pada kasus-kasus berikut, bagaimana cara menentukan kemiringan m pada suatu garis.

1. Kasus 1. kemiringan garis yang melalui dua titik.

2. Kasus 2. kemiringan garis yang saling sejajar terhadap satu garis tertentu.

3. Kasus 3. kemiringan garis yang saling tegak lurus terhadap satu garis tertentu.

Tuliskan hasil kerja kalian sejelas mungkin sehingga teman kalian akan mudah membacanya. Pamerkan hasil karya kalian untuk mendapatkan umpan balik dari teman-teman kalian.

Langkah-langkah Kegiatan Berpikir Kreatif ini diserahkan sepenuhnya kepada teman Guru untuk menyusunnya sendiri, sebagai latihan. Kemudian perkirakan sendiri juga kesimpulan yang diperoleh dari kegiatan ini. Atau jika tidak memungkinkan, jadikanlah sebagai tugas individu untuk dijadikan sebagai nilai tambahan untuk Ulangan Harian.

Disclaimer:

Kunci Jawaban pada unggahan kontempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 Soal Laihan 5.2 halaman 230 Pengertian Kemiringan. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.