kontenjempolan.id-Kunci Jawaban Soal Laihan 4.4 Halaman 198 Korespondensi Satu-satu (Pengayaan) Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 198. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 4 Relasi dan Fungsi.

Relasi dan Fungsi

Korespondensi Satu-satu (Pengayaan)

Soal Laihan 4.4

1. Manakah dari diagram panah berikut ini yang menggambarkan korespondensi satu-satu? Jelaskan.

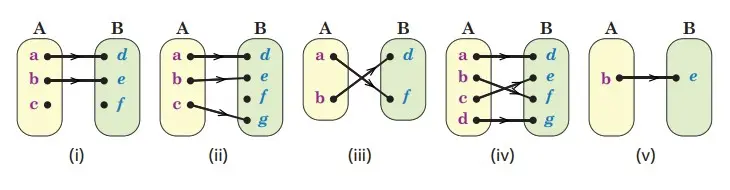
Jawaban:

Alternatif Jawaban:

Dari diagram panah yang menunjukkan korespondensi satu-satu adalah (iii), (iv) dan (v)

2. Manakah di antara himpunan pasangan berurutan berikut yang termasuk korespondensi satu-satu? Jelaskan.

a. {(1 , 1); (2 , 2); (3 , 3)}

b. {(2 , 2); (2 , 4); (2 , 6)}

c. {(a , 2); (2 , b); (b , a)}

d. {(1 , p); (2 , q); (3 , p)}

e. {(5 , 6); (6 , 7); (7 , 5)}

f. {(a , x); (b, z); (a , y)}

Jawaban:

“Serahkan kepada teman Guru”

a. {(1 , 1); (2 , 2); (3 , 3)}

Anggota A = {1. 2. 3} Anggota B = {1, 2, 3}

c. {(a , 2); (2 , b); (b , a)}

Anggota A = {a. 2. b} Anggota B = {2, b, a}

e. {(5 , 6); (6 , 7); (7 , 5)}

Anggota A = {5. 6. 7} Anggota B = {6, 7, 5}

Alasan: Setiap anggota dari daerah asal maupun dari daerah kawan hanya mempunyai satu pasang.

Ayo Berpikir Kritis

3. Subarno mengatakan bahwa setiap dua himpunan yang banyak anggotanya sama pasti selalu dapat dikatakan korespondensi satu-satu. Tetapi Sunardi tidak setuju dengan pendapat Subarno, karena dua himpunan yang dapat dinyatakan dengan korespondensi satu-satu memiliki hubungan yang khusus. Setujukah kalian dengan pendapat Sunardi? Jelaskan.

Jawaban:

Setuju dengan Subarno dan Sunardi, karena dua himpunan yang banyak anggotanya sama merupakan fungsi khusus yang dapat dikatakan sebagai korespondensi satu-satu

Ayo Berpikir Kreatif

4. Temukan kejadian sehari-hari di sekitar kalian yang menunjukkan sebagai korespondensi satu-satu. Presentasikan secara singkat temuan kalian di depan kelas.

Jawaban:

“Serahkan kepada teman Guru”

Siswa dengan nomor kartu Ujian

Siswa dengan Nomor Induk Siswa

5. Apabila diketahui banyak anggota dua himpunan seperti berikut ini, maka ada berapa banyak korespondensi satu-satu yang mungkin dari himpunan A dan himpunan B?

a. n(A) = n(B) = 12

b. n(A) = n(B) = 9

Jawaban:

Alternatif Jawaban:

a. Sebanyak 12! (faktorial)

b. Sebanyak 9! (faktorial)

6. Manakah diantara dua himpunan berikut ini yang dapat dinyatakan sebagai korespondensi satu-satu? Jelaskan.

a. A = {nama bulan dalam setahun}
B = {nama hari dalam seminggu}

b. C = {bilangan genap kurang dari 10}
D = {bilangan prima kurang dari 10}

c. E = {a, e, i, o, u}
F = {lima kota besar di Pulau Jawa}

d. G = {nama hari dalam seminggu}
H = {bilangan prima antara 1 dan 11}

Jawaban:

Himpunan berikut ini yang dapat dinyatakan sebagai korespondensi satu-satu

b. C = {bilangan genap kurang dari 10}
D = {bilangan prima kurang dari 10}

Anggota himpunan C adalah {2, 4, 6, 8} dan anggota himpunan D adalah {2, 3, 5, 7}, sehingga banyak anggota keduanya dapat kita tulis n(C) = 4 dan n(D) = 4.

Jadi, banyak anggota keduanya sama, sehingga dapat dinotasikan dengan n(P) = n(Q). Dengan demikian, himpunan C dan himpunan D merupakan korespondensi satu-satu.

c. E = {a, e, i, o, u}
F = {lima kota besar di Pulau Jawa}

Anggota himpunan E adalah {a, e, i, o, u} dan anggota himpunan F adalah {lima kota besar di Pulau Jawa}, sehingga banyak anggota keduanya dapat ditulis n(C) = 5 dan n(D) = 5.

Jadi, banyak anggota keduanya sama, sehingga dapat dinotasikan dengan n(E) = n(F). Dengan demikian, himpunan E dan himpunan F merupakan korespondensi satu-satu.

7. Diketahui himpunan K = {1, 2, 3, 4, 5, 6} dan himpunan L = {a, b, c, d, e, f }.

a. Tentukan ada berapa banyak korespondensi satu-satu yang mungkin dapat dibuat dari himpunan K ke himpunan L?

b. Coba minimal tiga himpunan pasangan berurutan yang termasuk korespondensi satu-satu dari himpunan K ke himpunan L.

Jawaban:

a. Diketahui himpunan K = {1, 2, 3, 4, 5, 6} dan himpunan L = {a, b, c, d, e,f} , sehingga didapat banyak anggotanya adalah n(K) = 6 dan n(L) = 6

Jadi, banyaknya korespondensi satu-satu dari himpunan K ke himpunan L adalah sebanyak n(K)! = n(L)! = 6!

6! = 6x 5 × 4 × 3 × 2 × 1 = 720.

b.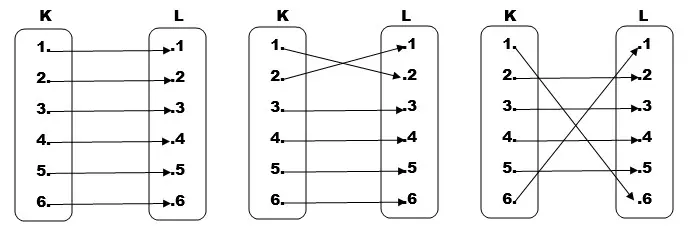

8. Jika diketahui himpunan A = {-2, -1, 0, 1, 2} , maka apakah fungsi f : A A yang dideinisikan sebagai berikut merupakan korespondensi satu-satu?

a. f : x -x

b. f : x x2

c. f(x) = 2×2 – 1

Jawaban:

“Serahkan kepada teman Guru”

9. Berdasarkan himpunan yang diberikan berikut, ada berapa banyak korespondensi satu-satu yang mungkin dapat dibuat?

a. Himpunan P = {huruf vokal} dan Himpunan Q = {bilangan cacah antara 1 dan 7}

b. Himpunan A = {faktor dari 8} dan Himpunan B = {faktor dari 21}

Jawaban:

a. Diketahui himpunan P = {a, i, u, e, o} dan himpunan Q = {2, 3, 4, 5, 6} , sehingga didapat banyak anggotanya adalah n(P) = 5 dan n(Q) = 5

Jadi, banyaknya korespondensi satu-satu dari himpunan K ke himpunan L adalah sebanyak n(P)! = n(Q)! = 5!

5!= 5 × 4 × 3 × 2 × 1 = 120.

b. Diketahui himpunan A = {1, 2, 4, 8} dan himpunan B = {1, 3, 7, 21} , sehingga didapat banyak anggotanya adalah n(A) = 4 dan n(B) = 4

Jadi, banyaknya korespondensi satu-satu dari himpunan K ke himpunan L adalah sebanyak n(A)! = n(B)! = 4!

4! = 4 × 3 × 2 × 1 = 24.

10. Sebuah perusahaan memproduksi suatu produk dengan kode tanggal manufaktur tertentu. Tentukan: Jika ABCDEFGHIJ adalah korespondensi satu-satu dengan ketentuan 0 1 2 3 4 5 6 7 8 9 dan CDAHBJIG mewakili kode barang untuk tanggal pembuatan 23 – 07 – 1986.

a. kode barang untuk tanggal produksi:

1) 14 April 1982

2) 27 Oktober 2021

b. tanggal produksi barang untuk kode:

1) CDAFCAAB

2) BDAEBJIE

Jawaban:

Diketahui:

A, B, C, D, E, F, G, H, I, J
0, 1, 2, 3, 4, 5, 6, 7, 8, 9

a. kode barang untuk tanggal produksi:

1) 14 April 1982 = BEAEBJIC

2) 27 Oktober 2021 = CHBACACB

b. tanggal produksi barang untuk kode:

1) CDAFCAAB = 23 Mei 2001

2) BDAEBJIE = 13 April 1984

 

Disclaimer:

Kunci Jawaban pada unggahan kontempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 Soal Laihan 4.4 halaman 198 Korespondensi Satu-satu (Pengayaan). Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.