kontenjempolan.id-Kunci Jawaban Soal Laihan 2.2 halaman 74 Tripel Pythagoras Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 74. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 2 Teorema Pythagoras.

Tripel Pythagoras

Soal Laihan 2.2

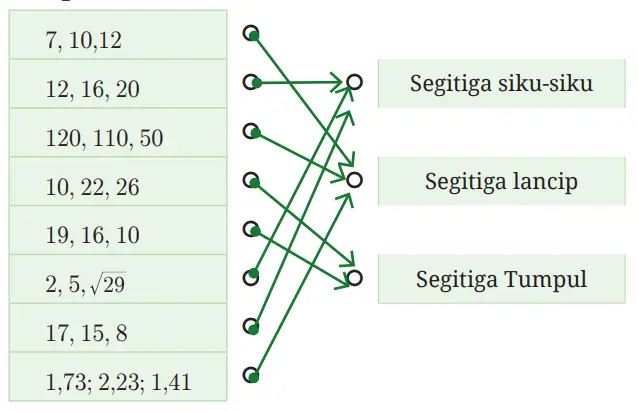
1. Sesuaikan tiga bilangan berikut dengan pasangan yang sesuai apakah termasuk segitiga siku-siku, segitiga lancip, dan segitiga tumpul.

Jawaban:

Pasangan Yang Sesuai

2. Buktikan bahwa diantara kelompok tiga bilangan berikut manakah yang merupakan tripel Pythagoras.

a. 24, 17, 25

b. 7, 13, 11

c. 6, 2 1/2, 6 1/2

Jawaban:

Kesimpulan.

a. Tripel Pythagoras

b. Bukan Tripel Pythagoras

c. Bukan Tripel Pythagoras

3. Ayo Berpikir Kreatif

Seekor kucing berada di atas genting dan terlihat kebingungan karena tidak bisa turun. Aysha yang melihat kucing tersebut langsung mencari galah dan kemudian diikat dengan keranjang kecil pada ujung galah tersebut. Saat menolong kucing tersebut, Cintia melihat Aysha dan mencoba membantunya untuk mengarahkan galah yang telah diikat keranjang tepat pada titik lokasi kucing pada jarak 4 meter. Jika jarak pandangan Cintia terhadap kucing diperkirakan 5 meter. Tentukan hasil dari pernyataan berikut ini.

a. Tentukan jarak atap yang ditempati kucing terhadap tanah tempat Aysha berdiri.

b. Tentukan panjang galah yang digunakan Aysha menolong kucing, jika tinggi Aysha 165 cm.

Jawaban:

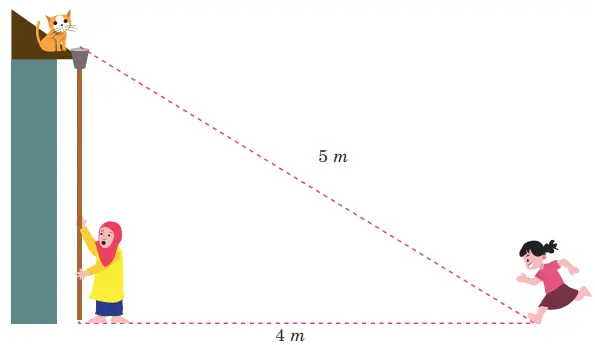
a. Jarak kucing dengan tanah

= √(5² – 4²)
= √(25 – 16) = √9 = 3

Sehingga, jarak kucing ke tanah adalah 3 m.

b. Tinggi Aysha 165 cm,

maka panjang galah adalah 3 m – 1,65 m =1,35 m

4. Ayo Berpikir Kritis

Kusen jendela yang berbentuk persegi panjang memiliki tinggi 40,8 cm dan panjang 30,6 cm, serta panjang salah satu diagonalnya 52,5 cm. Apakah kusen jendela benar-benar persegi panjang? Jelaskan.

Jawaban:

Kusen jendela akan membentuk persegi panjang, jika keempat sudutnya siku-siku. Untuk membuktikan bahwa setiap sudut pada kusen siku-siku maka perlu memanfaatkan Tripel Pythagoras.

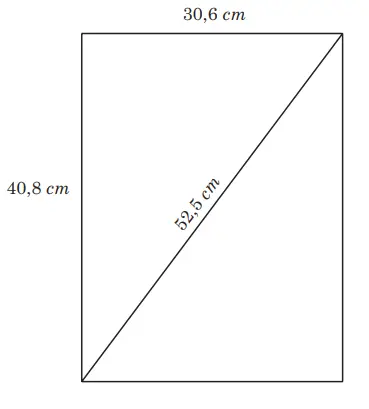
Berdasarkan gambar di atas, harus kita buktikan bahwa 52,5² = (40,8)² + 30,6²

Tripel Pythagoras terjadi jika c² = a² + b² ,c kita misalkan panjang diagonal

c² = (40,8)² + (30,6)²

C² = 1664,64 + 936,36 = 2601

C = V2601 = 51

Akan menjadi siku-siku jika panjang diagonal adalah 51 cm. Karena kusen pada soal 52,5 cm. Maka kusen jendela tersebut tidak membentuk persegi panjang.

5. Jika (p – q), p, (p + q) membentuk tripel Pythagoras,

a. Tentukan hubungan antara p dan q.

b. Jika p = 12, tentukan tripel Pythagoras.

Jawaban:

Jika divisualisasikan, maka bentuk (p – q), p, (p + q) menjadi

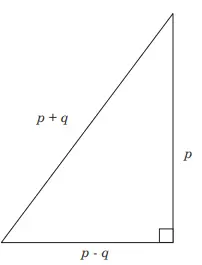
a. Berdasarkan gambar di atas, dapat digunakan aturan Teorema Pythagoras yaitu.

(p – q)² + p² = (p + q)²

p² – 2pq + q² + p² = p² + 2pq + q ²

2p² – p² = 2pq + 2pq + q² – q² = 0

p² – 4pq = 0

p(p- 4q) = 0

Maka nilai p adalah p = 0 atau p – 4q = 0, p = 4q

Sehingga, hubungan antara p dan q adalah p = 4q

b. Jika p = 12, menggunakan hubungan pada poin a, maka nilai q adalah

p = 4q
12= 4q
12/4 = q
q = 3

Karena p = 12 dan q = 3, Tripel Pythagorasnya adalah
(12 – 3)² + 12² = (12 + 3)²
9² + 12²

Sehingga, 9, 12, 15 merupakan Tripel Pythagoras

Disclaimer:

Kunci Jawaban pada unggahan kontempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 Ayo Berpikir Kritis halaman 73 Tripel Pythagoras. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.