Kunci Jawaban Latihan 4.4 Halaman 105 Kegunaan Perbandingan Trigonometri Tan θ Matematika SMA/SMK Kelas 10 Kurikulum Merdek
kontenjempolan.id-Kunci Jawaban Latihan 4.4 Halaman 105 Kegunaan Perbandingan Trigonometri Tan θ Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.
Latihan 4.4
Soal Pemahaman
1. Diketahui tan 
Gambarlah sebuah segitiga siku-siku yang memenuhi nilai perbandingan tersebut. Berikan label dan panjang sisi depan serta sisi sampingnya dalam cm!
Jawaban:
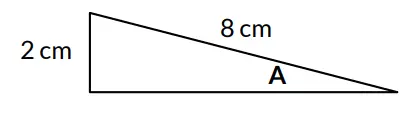
2. Cari panjang x !
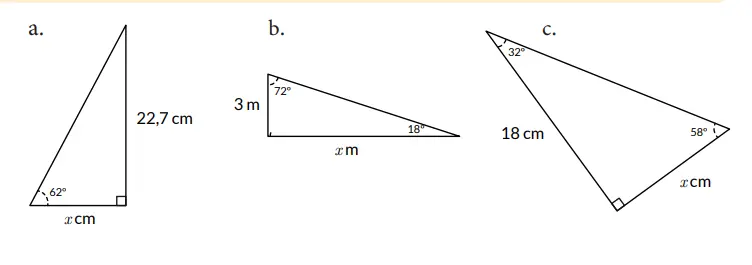
Jawaban:
a. x = 12.07 cm
b. x = 9.23 cm
c. x = 11.25 cm
3. Soal ini terdiri dari empat bagian.
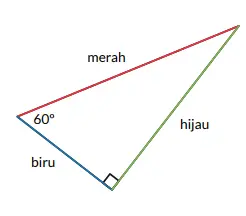
Bagian pertama:
Perhatikan segitiga berikut dan tentukan nama sisinya berdasarkan sudut 60º!
a. Sisi berwarna merah adalah sisi__________.
b. Sisi berwarna hijau adalah sisi __________.
c. Sisi berwarna biru adalah sisi __________.
Jawaban:
Bagian pertama:
a. Miring
b. Depan
c. Samping
Bagian kedua:
Segitiga berikut adalah segitiga yang sama dengan segitiga pada soal nomor pertama. Sekarang, tentukan nama sisinya berdasarkan sudut 30º!
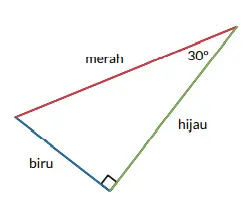
a. Sisi berwarna merah adalah sisi __________.
b. Sisi berwarna hijau adalah sisi __________.
c. Sisi berwarna biru adalah sisi __________.
Jawaban:
Bagian kedua:
a. Miring
b. Samping
c. Depan
Bagian ketiga:
Segitiga berikut adalah segitiga yang sama dengan segitiga pada soal nomor pertama dan kedua. Sekarang, tentukan nama sisi berdasarkan sudut yang ditentukan!
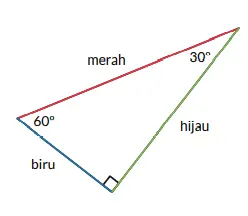
a. Sisi depan sudut 30º berwarna _______.
b. Sisi depan sudut 60º berwarna _______.
c. Sisi samping sudut 30º berwarna
Jawaban:
Bagian ketiga:
a. Biru
b. Hijau
c. Hijau
d. Biru
e. Merah
f. Merah
Bagian keempat:
Gunakan jawaban kalian pada soal nomor pertama untuk menyelesaikan permasalahan berikut.
a. Apakah sisi depan sudut 30º dan 60º sama atau berbeda? Mengapa demikian?
b. Apakah sisi samping sudut 30º dan 60º sama atau berbeda? Mengapa demikian?
c. Apakah sisi miring sudut 30º dan 60º sama atau berbeda? Mengapa demikian?
Jawaban:
a. Berbeda. Sisi depan sudut 30º dan 60º berbeda karena letak sudut yang berbeda.
b. Berbeda. Sisi samping sudut 30º dan 60º berbeda karena letak sudut yang berbeda.
c. Sama. Sisi miring sudut 30ºdan 60º sama karena definisi sisi miring adalah sisi di depan sudut siku-siku. Letak sudut siku-siku tidak berubah pada segitiga yang ditampilkan.
Soal Aplikasi
4. Diketahui tan 
a. Gambarlah dua segitiga siku-siku yang berbeda, namun tetap memenuhi nilai perbandingan tersebut.
Jawaban:
Siswa menggambar dua buah segitiga dengan sisi depan yang kali lebih panjang dari sisi samping berdasarkan letak ∠A pada segitiganya. Contoh jawaban yang tepat:
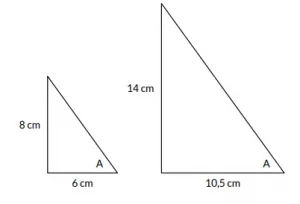
b. Apakah ada lebih dari dua segitiga yang memenuhi nilai perbandingan tersebut? Jelaskan alasanmu.
Jawaban:
Ya, ada lebih dari dua segitiga yang memenuhi nilai perbandingan tersebut. Ukuran segitiga dapat berubah asalkan perbandingan panjang sisinya sama, maka hasil tan ∠A juga akan tetap sama.
5. Seorang ahli perencana kota perlu membangun jalan dari titik B ke titik A.
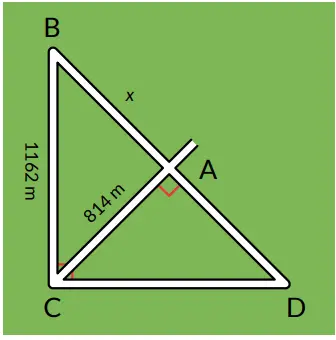
a. Cari panjang jalan yang perlu ia rencanakan untuk menghubungkan titik B ke A.
Jawaban:
Siswa perlu mengidentifikasi bahwa ∠BCA adalah 45o. Kemudian siswa dapat mencari bahwa tangen 45o = 1 di mana tangen adalah perbandingan sisi depan (x) dengan sisi CA. Jadi x = 814. Panjang jalan yang perlu direncanakan untuk menghubungkan titik B ke A adalah 814 meter.
b. Cari nilai perbandingan antara jarak titik C ke A dengan jarak titik C ke B.
Catatan: nilai Ini adalah nilai perbandingan trigonometri sinus.
Jawaban:
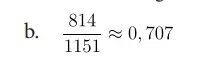
c. Cari nilai perbandingan antara jarak titik A ke B dengan jarak titik C ke B.
Catatan: nilai ini adalah nilai perbandingan trigonometri cosinus.
Jawaban:
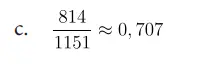
d. Jika segitiga ABC dan segitiga ADC sebangun, cari panjang CD!
Jawaban:
Segitiga sebangun mempunyai perbandingan nilai sisi yang sama. Karena segitiga ABC dan ADC mempunyai satu sisi yang sama panjang yaitu sisi CA (814 m) maka siswa dapat menyimpulkan bahwa panjang CD adalah sama dengan panjang BC. Panjang sisi CD sama dengan 1.151 m.
6. Seorang teknisi sedang memperbaiki sebuah menara pemancar yang mempunyai tinggi 150 meter. Jarak antara titik B dan D adalah 125 meter.
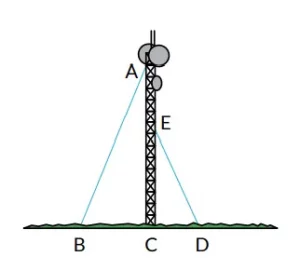
a. Jika sudut yang terbentuk oleh kedua tangga adalah 60o, hitung jarak BC!
Jawaban:
Panjang sisi AC adalah 150 m.
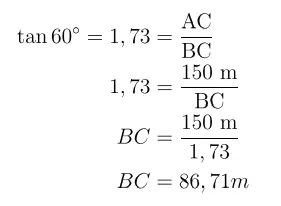
b. Cari juga jarak CD.
Jawaban:
Panjang CD dapat dicari dengan: 125 m – 86,71 m = 38,29 m
Soal Penalaran
7. Standar sudut mendarat pesawat yang direkomendasikan untuk kenyamanan dan kemulusan adalah 3o. Jika pesawat sedang berada di ketinggian 600 meter, berapa jarak antara posisi pesawat sekarang dengan posisi pendaratannya yang ideal?
Jawaban:
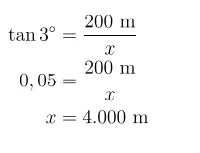
8. Seorang ahli bangun perlu mengukur jarak sungai untuk mempersiapkan pembangunan jembatan. Pertama, ahli bangun tersebut memberikan tanda di titik awalnya dan melihat ada pohon besar di seberang sungai. Ia kemudian berjalan sambil mengukur jarak, sampai posisinya sejajar dengan pohon. Jarak yang baru saja ia tempuh adalah 400 meter. Ia kemudian kembali ke titik awal dan mengukur sudut perputaran arah ke posisi pohon dengan theodolit. Ia mendapatkan sudut sebesar 31º.
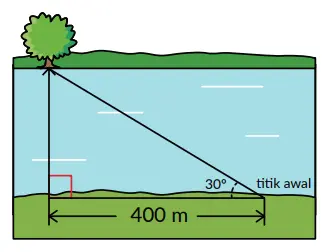
a. Tentukan panjang rancangan jembatan yang seharusnya berdasarkan informasi yang ada!
Jawaban:
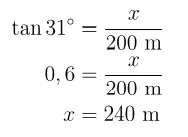
b. Untuk memastikan penghitungannya tepat, ahli bangun memilih titik awal yang berbeda dan mengukur jarak serta sudutnya. Ia mendapatkan sudut perputaran 36o serta jarak 330,8 meter. Tanpa melakukan penghitungan matematika, berikan penjelasan apakah strategi yang digunakan ahli bangun tersebut tepat atau tidak tepat.
Jawaban:
Strateginya tepat dan akan berguna untuk memastikan perhitungan yang akurat. Strategi ini berguna karena menggunakan penerapan perbandingan trigonometri yang sama dengan strategi awalnya. Yang dilakukan oleh ahli bangun adalah mencari data tambahan yang dapat memberikan konfirmasi atas data awalnya
9. Dimas sedang mencoba mencari tinggi tiang bendera. Dengan bantuan teman dan alat busur, ia memperkirakan sudut yang terbentuk antara kepala dan ujung tiang bendera adalah 34º.
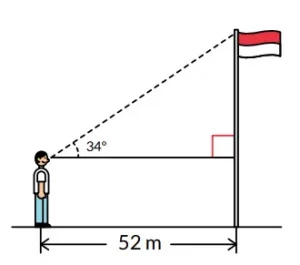
a. Jarak antara Dimas dan tiang bendera adalah 52 m. Cari panjang sisi depan berdasarkan sudut dan jarak yang diketahui!
Jawaban:
Panjang sisi depan dapat ditemukan dengan mencari nilai perbandingan trigonometri tangen.
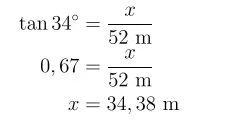
b. Teman Dimas beranggapan bahwa jawaban di bagian a merupakan tinggi tiang bendera yang sesungguhnya. Dimas tidak setuju dengan pernyataan itu. Bagaimana pendapat kalian? Jelaskan alasannya.
Jawaban:
Pernyataan teman Dimas tidak tepat. Panjang sisi depan tidak sama dengan 7tinggi tiang bendera karena tinggi Dimas perlu dimasukkan ke dalam perhitungan. Berdasarkan Gambar 4.28, segitiga yang terbentuk bermula dari ketinggian mata Dimas. Maka, untuk mencari tinggi tiang bendera, kita harus menambahkan tinggi Dimas.
Demikian pembahasan Matematika Kelas 10 SMA/SMK halaman 105 Latihan 4.4, Kegunaan Perbandingan Trigonometri Tan θ. Selanjutnya untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat diakses melalui kontenjempolan.id.



