kontenjempolan.id-Kunci Jawaban halaman 46 Aplikasi Sistem Persamaan Linear Dua Variabel (SPLDV) Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 46. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 2 Sistem Persamaan Linear Dua Variabel.

Aplikasi Sistem Persamaan Linear Dua Variabel (SPLDV)

Q. Di Jepang, Heru membeli 12 buah makanan yang terdiri dari kue dan puding dengan total harga 2.000 yen. Harga untuk 1 kue 200 yen dan 1 puding seharga 120 yen. Berapa banyak masing-masing kue dan puding yang dibeli?

Jawaban:

Jika x = kue, dan y = puding

x + y = 12
200x + 120y = 2000

Cara Subtitusi

x = 12 – y

200(12 – y) + 120y = 2000
2400 – 200y + 120y = 2000
-80 y = 2000 – 2400
-80y = -400
y = 5

⇔x + y = 12
x+ 5 = 12
⇔x = 7

Jadi Kue sebanyak 7 buah, dan Puding sebanyak 5 buah

Di , jika kita menggunakan sistem persamaan, maka kita dapat menyelesaikannya seperti berikut.

Hubungan antara banyaknya makanan tersebut adalah sebagai berikut.

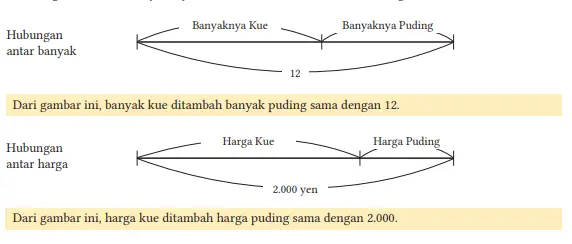
Soal 1

Dengan memisalkan banyaknya kue yang dibeli dengan x buah dan banyaknya puding yang dibeli adalah y buah, maka kita dapat menyelesaikan permasalahan dengan membentuk sistem persamaan dari hubungan antar harga tersebut.

Jawaban:

Jika banyak kue adalah x buah, dan puding adalah y buah, maka

x + y = 12
200x + 120y = 2.000

Maka

Jumlahnya, 7 + 5 = 12 (buah)

jumlah uangnya adalah 200 × 7 + 120 × 5 = 2.000 yen

Jadi, sesuai dengan soal bahwa kue 7 buah dan puding 5 buah.

Jawaban: Kue sebanyak 7 buah, puding sebanyak 5 buah.

Langkah-Langkah Penggunaan Sistem Persamaan untuk Menyelesaikan Masalah Kehidupan Sehari-hari

1) Cari hubungan antar kuantitas dalam soal, dan nyatakan dengan diagram, tabel, atau kata-kata.

2) Tentukan kuantitas apa saja yang diketahui dan apa yang tidak diketahui, kemudian bentuklah sistem persamaan menggunakan variabel yang tepat.

3) Selesaikan sistem persamaan yang diperoleh.

4) Periksa apakah penyelesaian sistem persamaan sudah menyelesaikan permasalahan atau belum.

Soal 2

Bagilah 35 peserta didik ke dalam beberapa kelompok dengan banyak anggota 4 orang dan 5 orang, sehingga total jumlah kelompok adalah 8. Untuk mencari banyaknya peserta didik pada setiap kelompok, kita akan memperhatikan “langkah-langkah penggunaan sistem persamaan untuk menyelesaikan masalah pembagian kelompok” di atas.

(1) Identifikasi hubungan antarkuantitas dalam soal, dan lengkapi diagram berikut dengan cara mengisikan informasi yang diperlukan. Dengan menggunakan diagram yang telah dilengkapi, nyatakan hubungan antarkuantitas menggunakan persamaan-persamaan.

Hubungan antara banyaknya kelompok

Hubungan antara banyaknya orang

Jawaban:

Hubungan jumlah kelompok

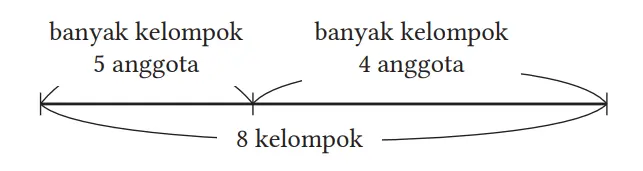
(Kata-kata)

(Banyak kelompok 5 anggota) + (Banyak kelompok 4 anggota) = 8 kelompok

– Hubungan jumlah orang

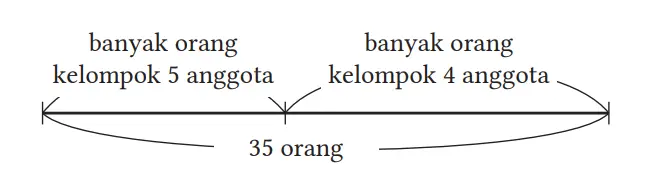
(Kata-kata)

(Banyak orang kelompok 5 anggota) + (Banyak orang kelompok 4 anggota) = 35 orang

(2) Nyatakan kuantitas yang tidak diketahui dengan variabel, dan bentuklah sistem persamaan menggunakan diagram yang digunakan di 1 .

Jawaban:

Banyak kelompok 5 anggota adalah x, banyak kelompok 4 anggota adalah y, maka

x + y = 8
5x + 4y = 35

(3) Selesaikan sistem persamaan linear yang diperoleh di 2 .

Jawaban:

x = 3
y = 5

(4) Periksa apakah penyelesaian dari sistem persamaan sudah menjawab permasalahan, dan carilah jawaban dari soal yang ditanyakan.

Jawaban:

Total jumlah kelompok adalah

3 + 5 = 8 (kelompok)

Total jumlah orang:

5 × 3 + 4 × 5 = 35 (orang)

Kelompok beranggota 5 orang ada 3 kelompok, kelompok beranggota 4 orang ada 5 kelompok, sesuai dengan soal.

Jawaban: Banyak kelompok beranggota 5 orang ada 3 kelompok dan banyak kelompok beranggota 4 orang ada 5 kelompok.

Soal 3

Diketahui dua anak timbangan A dan B berbeda berat. Berat 3A dan 2B adalah 190 g, berat 4A dan 6B adalah 320 g. Berapakah berat sebuah anak timbangan A dan sebuah anak timbangan B?

Jawaban:

Jika berat 1 buah A adalah x g, dan berat 1 buah B adalah y g, maka

3x + 2y = 190
4x + 6y = 320

Penyelesaiannya: x = 50, dan y = 20

Jadi, 1 buah A beratnya 50 g, dan berat 1 buah B adalah 20 g.

Jawaban: 1 buah A mempunyai berat 50 g dan 1 buah B mempunyai berat 20 g.

Contoh 2

Saya menempuh perjalanan dari rumah ke stasiun kereta api sejauh 12 km. Mula-mula, saya bersepeda dengan kecepatan 18 km/jam, tetapi kemudian ban sepeda saya kempes di perjalanan. Karena itu, saya berjalan ke stasiun dengan kecepatan 4 km/jam. Total waktu yang saya perlukan hingga sampai ke stasiun adalah 1 jam 15 menit. Tentukan jarak tempuh bersepeda, dan jarak tempuh jalan kaki.

Dengan menyatakan hubungan antarkuantitas menggunakan diagram, kita memperoleh diagram berikut ini.

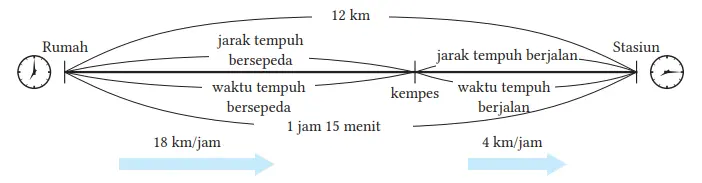
Menggunakan hubungan antarkuantitas, jika kita misalkan jarak bersepeda adalah x km dan jarak jalan kaki adalah y km, maka kita peroleh berikut.

Dengan memisalkan jarak bersepeda x km dan jarak berjalan kaki y km, kita peroleh

x + y = 12
x/18 + y/4 = (75/60)

(1) × 2 2x + 2y = 24
(2) × 36 2x + 9y = 45|-|
–7y = –21
y = 3

Substitusi y = 3 ke 1 , maka diperoleh

x + 3 = 12
x = 9

Jarak bersepeda 9 km, dan jarak berjalan kaki 3 km. Hal ini sudah menjawab soal.
Jawaban: Jarak bersepeda adalah 9 km, dan jarak berjalan kaki adalah 3 km.

Soal 4

Pada Contoh 2, misalkan waktu tempuh bersepeda adalah x jam, dan waktu tempuh berjalan kaki adalah y jam. Buatlah sistem persamaan dan carilah penyelesaiannya.

Jika disusun lama waktu tempuh dengan menggunakan sepeda adalah x jam, dan lama waktu tempuh dengan berjalan kaki adalah y jam, berdasarkan hubungan jumlah, maka diperoleh tabel berikut.

Penyelesaiannya:

x = 1/2, dan y = 3/4

18 × 1/2 = 9, 4 × 3/4 = 3

Jarak tempuh dengan sepeda adalah 9 km, dan jarak tempuh dengan berjalan kaki adalah 3 km, maka sesuai dengan soal.

Jawaban: Jarak tempuh dengan sepeda 9 km. Jarak tempuh berjalan kaki 3 km.

Soal 5

Saya berkendara dari kota A ke kota B sejauh 90 km. Kendaraan melaju dengan kecepatan 80 km/jam di jalan tol dan 50 km/jam di jalan biasa, dan waktu yang saya butuhkan adalah 1 jam 30 menit. Carilah jarak yang ditempuh di jalan tol dan jarak tempuh di jalan biasa.

Jawaban:

Jika menempuh perjalanan di jalan tol adalah x km, dan menempuh perjalanan di jalan biasa y km, maka

x + y = 90
x/80 + y/50 = 1 30/60

Penyelesaiannya: x = 40, dan y = 50

Jarak tempuh di jalan tol adalah 40 km, dan jarak tempuh di jalan umum adalah 50 km, sesuai dengan soal.

Jawaban: Jarak tempuh di jalan tol 40 km. Jarak tempuh jalan biasa 50 km.

Soal 6

Total banyaknya peserta didik laki-laki dan peserta didik perempuan di suatu SMP tahun lalu adalah 220 peserta didik. Tahun ini peserta didik laki-laki mengalami kenaikan sebesar 5%, sedangkan banyaknya peserta didik perempuan mengalami penurunan sebesar 2%. Secara keseluruhan, banyaknya peserta didik mengalami kenaikan sebesar 4 orang.

(1) Carilah banyaknya peserta didik laki-laki dan peserta didik perempuan tahun lalu.

Jawaban:

Jika banyak peserta didik laki-laki tahun lalu x orang, dan banyak peserta didik perempuan adalah y orang, maka

x + y = 220
5/100 x – 2/100y = 4

Penyelesaiannya: x = 120, dan y = 100

Banyak peserta didik laki-laki tahun lalu adalah 120 orang, dan peserta didik perempuan 100 orang, telah sesuai dengan soal.

Jawaban: Banyak peserta didik laki-laki tahun lalu adalah 120 orang

Banyak peserta didik perempuan tahun lalu adalah 100 orang.

(2) Carilah banyaknya peserta didik laki-laki dan peserta didik perempuan tahun ini.

Jawaban:

120 × 105/100 = 126
100 × 98/100 = 98

Jawaban: Banyak peserta didik laki-laki tahun ini adalah 126 orang.

Banyak peserta didik perempuan tahun ini adalah 98 orang.

Soal 7

Sebanyak 200 g larutan garam 15% dibuat dengan mencampur larutan garam 12% dan larutan garam 20%. Berapa gram garam yang diperlukan masing-masing larutan garam 12% dan larutan garam 20%?

Jawaban:

Jika larutan garam 12% sebanyak x g, dan larutan garam 20% sebanyak y g, maka
x + y = 200
12/100x + 20/100y = 200 × 15/100

Penyelesaiannya: x = 125, dan y = 75

Larutan garam 12% sebanyak 125 g, larutan garam 20% sebanyak 75 g, sesuai dengan soal.

Jawaban: Larutan garam 12% sebanyak 125 g.

Larutan garam 20% sebanyak 75 g.

 

Disclaimer:

Kunci jawaban pada unggahan kontenjempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 halaman 46 Aplikasi Sistem Persamaan Linear Dua Variabel (SPLDV). Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat diakses melalui kontenjempolan.id.