kontenjempolan.id-Ayo Bereksplorasi Halaman 239 Pengertian Kemiringan Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 239. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Persamaan Garis Lurus.

Kalian perlu mengetahui bentuk lain dari persamaan garis lurus. Perhatikan dengan cermat contoh 5.8 berikut ini.

Jika diketahui suatu garis melalui titik (-4, p) dan (1, 2) dengan kemiringan -3/4 , maka hitung nilai p.

Misalkan (-4, p) adalah (x1, y1) dan (1,1) adalah (x2, y2)

Diketahui kemiringan garisnya adalah -3/4.

Substitusi nilai tersebut ke rumus kemiringan garus, sehingga didapat sebagai berikut:

Kemiringan garis = (y2-y1)/(x2-x1) = -3/4

    -3/4 = (2-p)/(1-)-4)                substitusi nilai x dan y

    -3/4 = (2 – p)/5                       sederhanakan

(-3) x 5 = 4 (2-P)                         kalikan silang

     -15 = 8 – 4p                              sederhanakan

-15 – 8 = -4p                                 kurangkan kedua ruas oleh 8

     -23 = -4p                                 sederhanakan

    23/4 = p                                   bagi kedua ruas oleh -4

Coba terapkan hasil pembelajaranmu pada bentuk lain persamaan garis lurus yang melalui dua titik yaitu titik A(x1, y1) dan B(x2, y2), berdasarkan hasil pengamatan dan pembahasan pada materi persamaan garis lurus yang telah kalian pelajari.

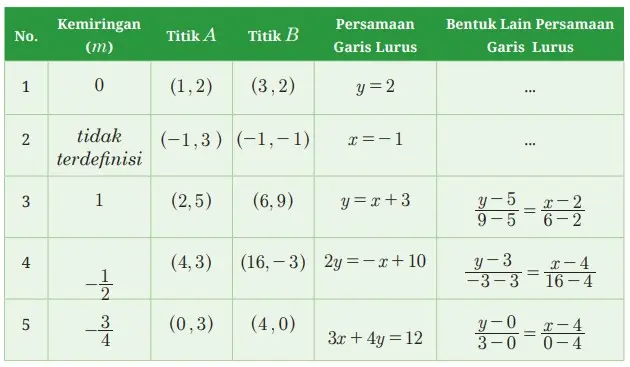
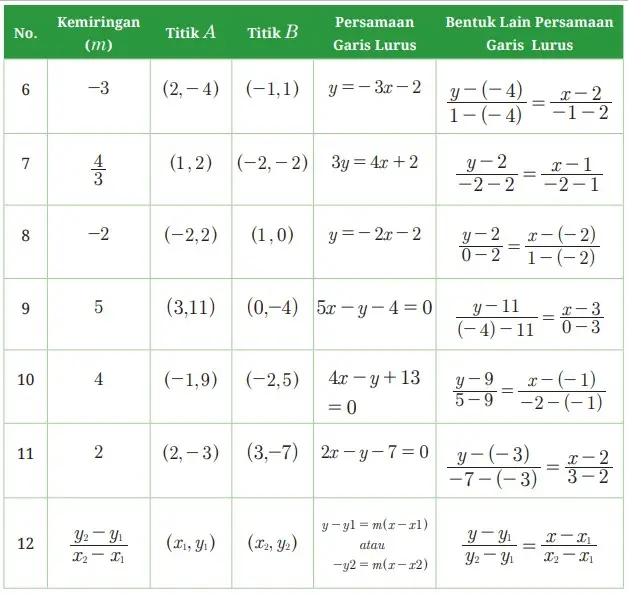
Berdasarkan hasil kegiatan diskusi kalian pada Tabel 5.4 di atas, usahakan untuk memastikan bahwa bentuk umum dari persamaan garis yang melalui dua titik A(x1, y1) dan B(x2, y2) dapat diketahui dengan pasti. Pada baris pertama dan kedua mengapa tidak diisi untuk bentuk lain persamaan garis lurus? Apakah hal ini ada berhubungannya dengan bentuk umum persamaan garis? Jelaskan tanggapan kalian.

Ketika koordinat dua titik yang dilalui garis diketahui, maka akan didapat suatu persamaan garis lurus tertentu. Lakukan yang terbaik untuk mendapatkan persamaan garis yang melalui (1,-5) dan (-2,4).

Pendekatannya dengan cara menggunakan rumus: (y – y1)/(y2 – y1) = (x – x1)/(x2 – x1)

Substitusi titik (1,-5) dan (-2,4) ke Persamaan rumusnya

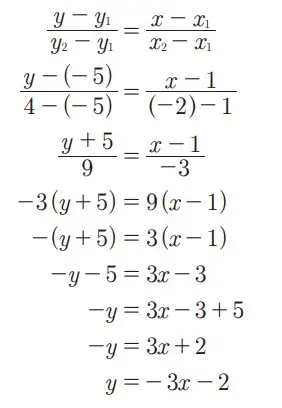
Jadi, persamaan garis yang melaui titik (1,-5) dan (-2,4) adalah y = -3x – 2

Pendekatan kedua dengan menggunakan rumus kemiringan garis lurus, yakni:

Kemiringan garis = (y2 – y1)/(x2-x1)

= 4 – (-5)/(-2-1)

= -3

Bentuk umum persamaan garis, yaitu y = mx + c , dan (-2,4)

sehingga didapat sebagai berikut:

y = mx + c

4 = -3(-2) + c

c = -2

Catatan: Hasil yang sama jika (1,-5) digunakan untuk menentukan nilai c

Pendekatan ketiga ini, yaitu menghitung kemiringan garis yang dimaksud dengan membandingkan dua bentuk aljabar.

P (x,y) dapat berupa sembarang titik pada garis. Akibatnya, kemiringan garis melalui titik (-2,4) dan P (x,y) adalah:

m = (y – 4)/(x-(2) = (y-4)/(x+2)

Sehingga, kemiringan garis kurus yang melalui titik (1,-5) dan (-2,4) adalah

m = (4 -(-5)/(-2-1) = -3

Dikarenakan nilai kemiringannya sama, maka didapat sebagai berikut:

(y-4)/(x+2) = -3

y-4 = -3(x + 2)                               kalikan kedua ruas oleh x + 2

y-4 = -3x – 6                                   sederhanakan

  y = -3x – 2                                     tambahkan kedua ruas oleh 4

Gambar 5.15 Graik persamaan y = -3x – 2

1. Ajaklah siswa untuk memahami ketiga jawaban siswa tersebut. Apabila diperlukan bahaslah secara klasikal dengan menuliskan dipapan tulis atau ditampilan dilayar LCD dari ketiga jawaban siswa tersebut. Berikan kesempatan kepada siswa untuk memutuskan, beserta justiikasinya, pilihan mana yang merupakan jawaban terbaik menurut pendapat mereka.

2. Instruksikan kepada siswa untuk saling berpasangan dengan teman sebelahnya, kemudian ajaklah siswa untuk saling berdiskusi.

3. Berilah tugas berupa soal yang senada kepada siswa untuk didiskusikan jawabannya dengan kelompok mareka masing-masing (berilah jawaban yang komunikatif).

4. Tukarkan hasil jawaban soal tersebut (soal yang ditugaskan) dengan kelompok lain, kemudian berilah argumennya (apakah semua anggota kelompok memahami jawaban dari kelompok lain?). kemudian, instruksikan kepada siswa untuk menuliskan kesimpulan dari hasil kegiatan ini.

Kunci Jawaban pada unggahan kontempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama