kontenjempolan.id-Kunci Jawaban Soal Laihan 2.3 halaman 81 Segitiga Istimewa Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 81. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 2 Teorema Pythagoras.

Segitiga Istimewa

Soal Laihan 2.3

1. Berikut ditunjukkan gambar rencana bangun rumah yang sedang dikerjakan oleh Amri sebagai seorang arsitek yang terlihat tampak depan.

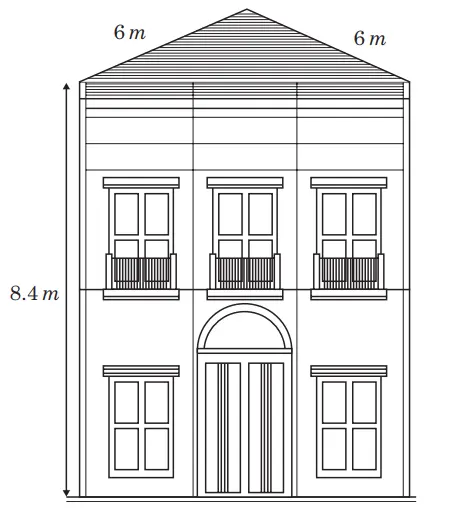
Tentukan tinggi atap rumah di atas, jika lebar rumah adalah 6.4 meter.

Jawaban:

Berdasarkan gambar, atap kerangka rumah dapat divisualisasi seperti gambar berikut.

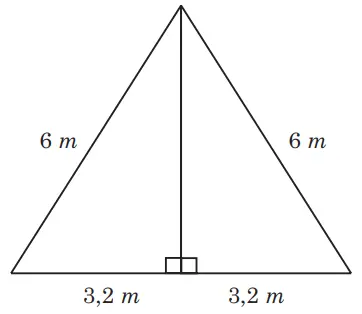
tinggi atap = √(6² – 3,2²)
                      = √(36 – 10,24)
                      = √25,76 = 5,075 m

Sehingga tinggi atap adalah 5,075 m

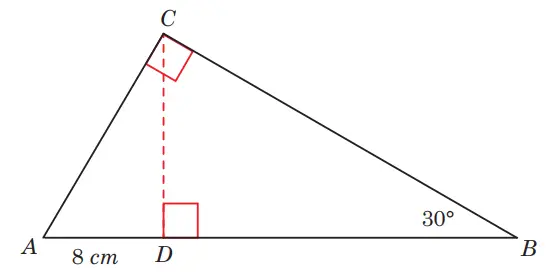
2. Bagaimana kalian dapat menemukan nilai x dan y pada bangun datar berikut.

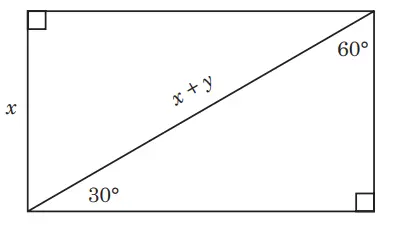
Jawaban:

Gambar disederhanakan menjadi bentuk berikut.

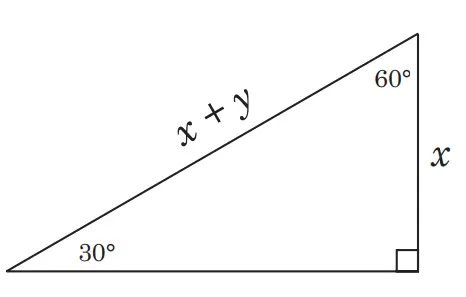
Menggunakan aturan sudut istimewa berikut

Maka 2x = x + y
2x – x = y
x = y

Sehingga x = y

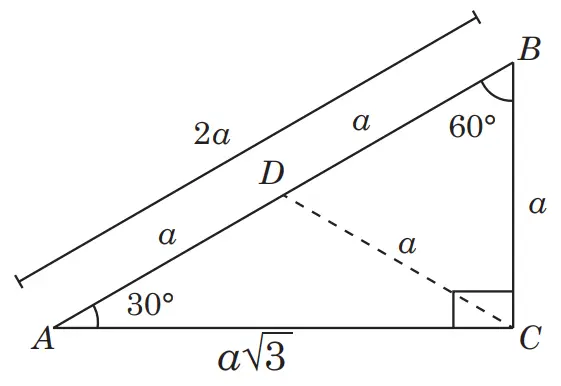
3. Perhatikan gambar segitiga siku-siku ABC di samping.

Tentukan
a. Keliling segitiga ABC.

b. Tentukan luas segitiga ABC.

Jawaban:

Menggunakan aturan segitiga istimewa siku-siku dengan sudut 30°, 90° dan 60°

a. Keliling segitiga ABC

kel = CA + AB + BC

Kel= 16 + 32 + 16√3 = (48 + 16√3) cm

b. Tentukan luas segitiga ABC

Luas segitiga ABC = 1/2 x a x t
= 1/2 x 32 x 8√3
= 16 x 8√3 = 128√3 cm²

4. Suatu tembok pembatas berbentuk trapesium akan di cat dasar untuk diberikan gambar mural. Jika dalam satu kaleng cat dapat digunakan mengecat untuk 1 5, m² dengan harga Rp. 22.500,00.
Tentukan biaya yang harus dihabiskan untuk mengecat tembok tersebut.(√3 = 1,73)

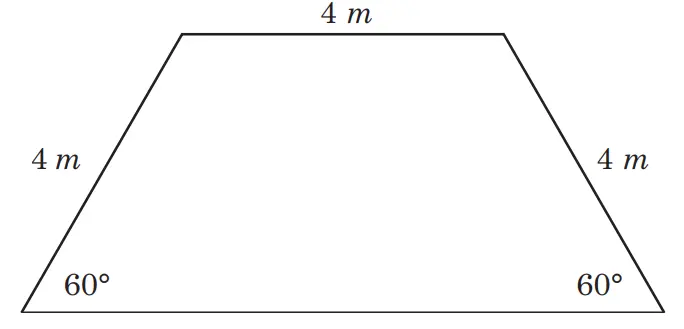
Jawaban:

Untuk menentukan sisi sejajar yang lain, harus ditemukan dahulu tinggi trapesium tersebut.

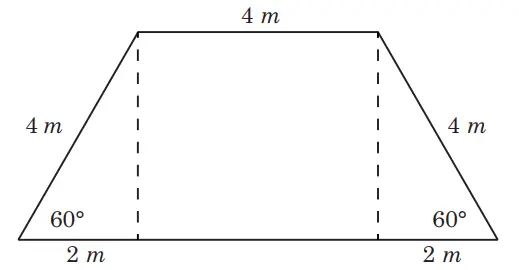
tinggi trapesium = √(4² – 2²)
= √(16 – 4)
= √12 = 2√3

Sehingga, sisi sejajar yang lain adalah 8 cm

Luastrapesium = 1/2 x (a + b) x t
= 1/2 x (4 + 8) x 2√3
= 1/2 x (12) x 2√3 = 12√3
Luas trapesium = 20.76

Karena setiap 1 5, m² menghabiskan cat dengan harga Rp.22.500, 00 maka biaya yang harus dikeluarkan adalah

biaya = 20,76/1,5 x 22500 = 311400

Sehingga, total biaya yang harus dikeluarkan adalah Rp. 311.400,00

5. Perhatikan gambar jaring-jaring piramida segitiga berikut.

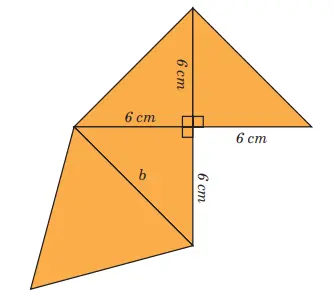
a. Tentukan panjang b.

b. Berapakah luas permukaan piramida segitiga tersebut?

Jawaban:

Menggunakan aturan segitiga istimewa pada segitiga siku-siku dengan sudut 45°, 90° dan 45°, maka.

a. Panjang b = 6√2 .

b. Luas permukaan piramida segitiga tersebut?

L Segitiga istimewa = 1/2 x a x t
L Segitiga istimewa = 1/2 x 12 x 6
= 6 x 6 = 36

Selanjutnya, luas segitiga sama sisi

Luas segitiga samasisi = 1/2 x a x t
Luas segitiga samasisi = 1/2 x 6√2 x 3√6
= 3√2 x 3√6 = 9√12

Luas segitiga samasisi = 18√3 cm²

Sehingga, luas permukaan piramida segitiga adalah (18 + 18√3) cm²

Disclaimer:

Kunci Jawaban pada unggahan kontempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 Soal Laihan 2.3 halaman 81 Segitiga Istimewa. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.