kontenjempolan.id-Kunci Jawaban Beragam Peluang halaman 181 Peluang Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 181. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 6 Peluang.

Peluang

Beragam Peluang

Q. Bila dua uang logam A dan B dilempar bersamaan, berapakah peluang munculnya 1 angka dan 1 gambar?

Jawaban:

2/4 = 1/2

Kita dapat berpikir tentang kasus dua uang logam yang dilempar dan munculnya gambar atau angka seperti berikut.

Ada dua kasus yang mungkin ketika melempar uang logam A, yaitu gambar atau angka. Hal ini berlaku pula bagi uang logam B. Oleh karena itu, seperti tampak pada tabel atau diagram berikut, maka akan ada (2 × 2) total kasus yang akan terjadi.

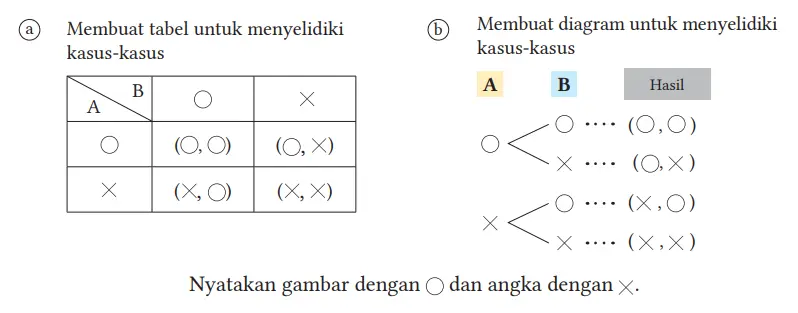
Diagram seperti pada (b) dinamakan diagram pohon. Dalam kasus ini, masing-masing dari empat kasus ((O ,O ), (O ,X ), ( X,O ), (X ,X )) memiliki kemungkinan yang sama untuk terjadi. Di antara mereka, terdapat dua kasus, yaitu (O ,X ), (O ,X ) yang memuat 1 gambar dan 1 angka, sehingga peluangnya adalah 2/4 = 1/2

Soal 1

Diketahui dua uang logam A dan B dilempar bersamaan. Tentukanlah nilai peluang dari tiap kejadian berikut.

(1) Kejadian munculnya dua gambar

Jawaban:

1/4

(2) Kejadian munculnya dua angka

Jawaban:

1/4

Soal 2

Diketahui tiga uang logam A, B, dan C dilempar bersama-sama. Tentukanlah nilai peluang munculnya kejadian dua gambar dan satu angka dengan menggunakan diagram pohon.

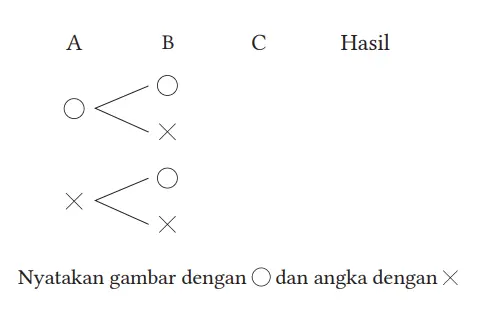
Jawaban:

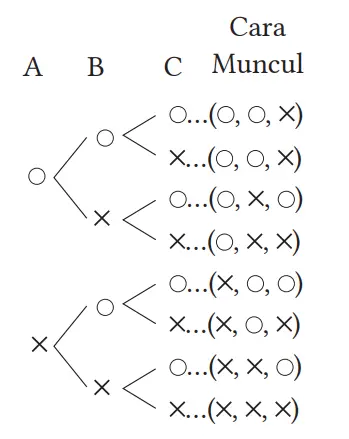
Total ada 2 × 2 × 2 = 8 cara. Dari jumlah tersebut, jika dua berada di depan dan dua di belakang, ada tiga cara: ( O,O ,X ), (O ,X ,O ), (X ,O ,O ), jadi peluangnya adalah 3/8.

Soal 3

Dua orang A dan B bermain “Kertas-Batu-Gunting” satu kali. Tentukanlah peluang bila kedua pemain tersebut bermain seri, dengan menggunakan diagram pohon. Anggaplah bahwa kedua pemain memiliki kemungkinan yang sama.

Jawaban:

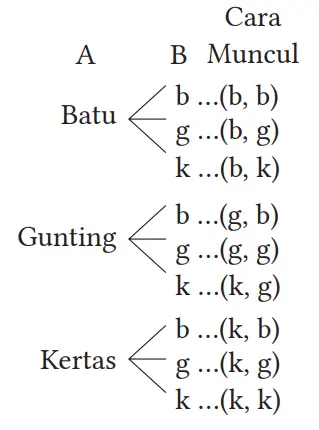
Total ada 3 × 3 = 9 cara. Dari jumlah tersebut, ada tiga cara untuk menjadi seri sehingga peluangnya adalah 3/9 = 1/3.

Soal 4

Dua dadu berbeda ukuran dilempar bersamaan. Jawablah pertanyaan-pertanyaan berikut.

(1) Tentukan peluang kejadian jumlah dua mata dadu 4.

Jawaban:

Jika jumlah angka mata dadu adalah 4, maka ada 3 cara (1, 3), (2, 2), dan (3, 1), sehingga peluang yang ditemukan adalah 3/36 = 1/12.

(2) Tentukan peluang kejadian jumlah dua mata dadu paling sedikit 10.

Jawaban:

Jika jumlah angka mata dadu 10 atau lebih, maka ada 6 cara (4, 6), (5, 5), (5, 6), (6, 4), (6,5), (6, 6), sehingga peluang yang ditemukan adalah 6/36 = 1/6.

(3) Peluang kejadian jumlah dua mata dadu manakah yang terbesar?

Jawaban:

Jumlah angka mata dadu adalah 7.

(Peluangnya adalah 6/36 = 1/6)

Contoh 2

Ada sebuah undian dengan 2 tiket berhadiah dan 3 tiket tidak berhadiah dalam sebuah wadah. A mengambil sebuah tiket dari wadah ini tanpa pengembalian dan B mengambil tiket lain. Dalam kasus ini, tentukan peluang kejadian bahwa A akan memperoleh tiket berhadiah.

Cara

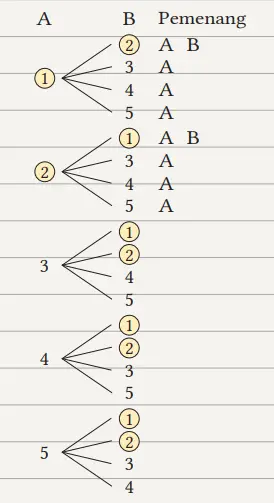
Misalkan tiket berhadiah adalah (1) dan (2) , dan tiket tidak berhadiah adalah 3, 4, dan 5. Kemudian, buatlah diagram pohonnya.

Penyelesaian

Bila A dan B mengambil masing-masing satu tiket dari wadah dengan urutan seperti pada cerita di atas, maka seperti diperlihatkan pada diagram pohon di sebelah kanan, akan terdapat 20 kejadian. Tiap kejadian memiliki peluang muncul yang sama. Di antara 20 kejadian ini, ada 8 kejadian agar A memperoleh tiket berhadiah.

Jadi, (Peluang A mendapat tiket berhadiah) =8/20 = 2/5

Soal 5

Pada Contoh 2, tentukan peluang bahwa B akan memperoleh tiket berhadiah. Bandingkan hasilnya dengan peluang A memperoleh tiket berhadiah. Tentukan pula peluang kedua orang tersebut memperoleh tiket berhadiah.

Jawaban:

Karena kejadian B memperoleh tiket berhadiah ada 8 cara, yaitu (1, 2), (2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (5, 1), dan (5, 2) maka peluang yang kita temukan adalah 8/20 = 2/5.

Dengan demikian, perbandingan peluang A dan B adalah sama besar. Selain itu, karena kejadian A dan B memperoleh tiket berhadiah ada 2 cara, maka peluang yang kita temukan adalah 2/20 = 1/10.

Soal 6

Pada Contoh 2, bila ada 3 tiket berhadiah dan 2 tiket tidak berhadiah, tentukanlah peluang bahwa A akan memperoleh tiket berhadiah dan peluang B memperoleh tiket berhadiah.

Jawaban:

Jika 1, 2, 3 yang meleset kita jadikan 4, 5, maka

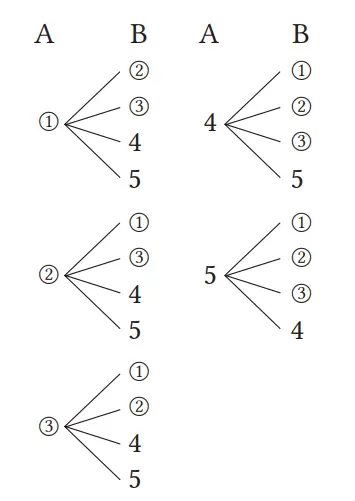
Peluang A memperoleh tiket berhadiah adalah 12/10 = 3/5

Peluang B memperoleh tiket berhadiah adalah 12/20 = 3/5

Soal 7

Ada tiga kartu dan salah satu kartu tersebut merupakan tiket berhadiah. Bila ada tiga orang mengambil tiga kartu tersebut dalam urutan tertentu tanpa pengembalian, apakah peluang memperoleh kartu berhadiah bergantung pada urutan pengambilan? Jelaskan jawabanmu berdasarkan gagasan peluang.

Jawaban:

Jika yang cocok 1, yang meleset menjadi 2, 3

Contoh 3

Bila dua calon akan dipilih dari empat peserta didik, yaitu A, B, C, dan D secara acak, tentukan peluang bahwa peserta didik B dan peserta didik C akan terpilih.

Cara

Dalam hal ini, urutan pemilihan tidak berpengaruh. Sebagai contoh, kasus terpilihnya A kemudian B sama saja dengan kasus terpilihnya B kemudian A. Nyatakan hal ini dalam bentuk {A, B} dan tentukan semua kasus berbeda yang akan terjadi.

Penyelesaian

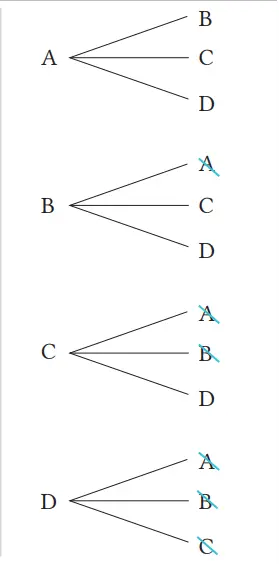
Untuk memilih 2 dari 4 peserta didik, ada enam kemungkinan, yaitu

{ A , B } , { A , C } , { A , D }, { B , C } , { B , D }, { C , D }

Setiap kemungkinan ini memiliki peluang yang sama. Di antara kemungkinan ini, ada satu kasus, yaitu {B, C}, yang mana B dan C terpilih. Oleh karena itu, peluang terpilihnya mereka adalah 1/6.

Jawaban: 1/6

Soal 8

Pada Contoh 3, tentukan peluang terpilihnya peserta didik D.

Jawaban:

Kejadian terpilihnya peserta didik ada 3 cara, yaitu

{A, D}, {B, D}, dan {C, D}.

Peluang yang kita temukan adalah 36 = 1/2.

Soal 9

Akan dipilih secara acak 2 tim dari 5 tim sepak bola yang berbeda, yaitu A, B, C, D, dan E. Tentukan peluang tiap kejadian berikut.

(1) Terpilihnya tim A dan E.

(2) Terpilihnya tim C.

Jawaban:

Cara terpilihnya 2 tim ada 10 cara, yaitu sebagai berikut.

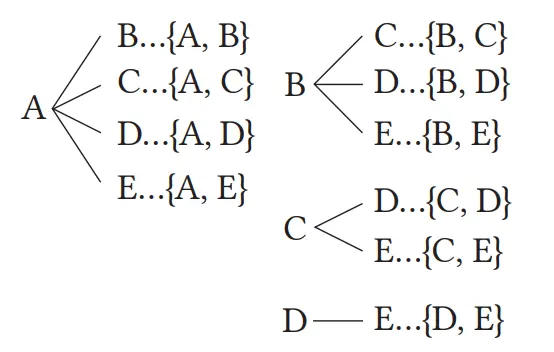
(1) Karena kejadian terpilihnya tim A dan E ada satu cara, yaitu (A, E), maka peluang yang akan kita temukan adalah 1/10.

(2) Karena kejadian terpilihnya C ada 4, yaitu {A, C}, {B, C}, {C, D}, {C, E}, maka peluang yang akan kita temukan adalah 4/10 = 2/5.

 

Disclaimer:

Kunci Jawaban pada unggahan kontenjempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 Beragam Peluang halaman 181 Bab 6 Peluang. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.