kontenjempolan.id-Kunci Jawaban Grafik Fungsi Linear halaman 66 Fungsi Linear Matematika SMP Kelas 8 Kurikulum Merdeka.

Hallo Adik-adik, kontenjempolan.id kali ini akan membahas materi Matematika SMP Kelas 8 halaman 66. Bacaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 3 Fungsi Linear.

Grafik Fungsi Linear

Q. Tabel berikut menunjukkan pasangan nilai x dan y dari fungsi y = 2x + 3. Berdasarkan tabel, gambarkan pasangan-pasangan bilangan x dan y tersebut pada bidang Cartesius berikut.

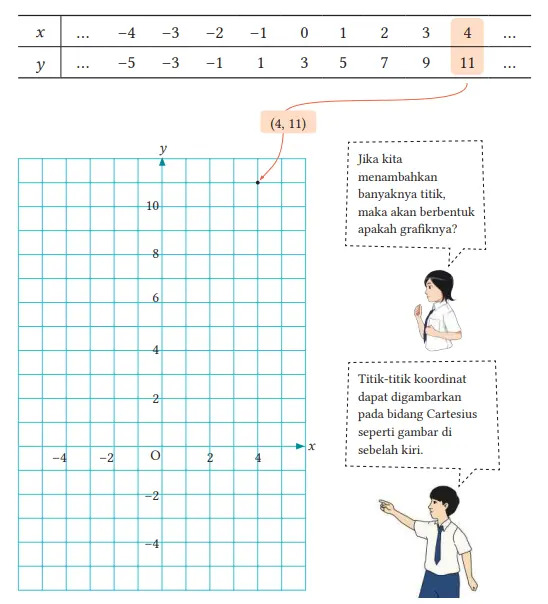
Ketika peserta didik belajar perbandingan senilai dan perbandingan berbalik nilai di kelas VII, peserta didik sudah belajar membuat tabel dan menggambar titik-titik pada bidang koordinat. Namun, beberapa peserta didik mungkin lupa bagaimana menggambar titik pada bidang koordinat.

Jadi, diharapkan peserta didik mengingatnya kembali dengan hati-hati sambil melihat kembali istilah seperti titik asal, koordinat x, dan koordinat y. Koordinat x juga dapat disebut nilai absis sedangkan koordinat y disebut ordinat.

Soal 1

Carilah nilai y yang berkorespondensi dengan nilai x yang berubah dari –4 hingga 4 sebesar 0,5. Juga, gambarkan koordinat-koordinat pasangan x dan y pada gambar di atas.

jawaban:

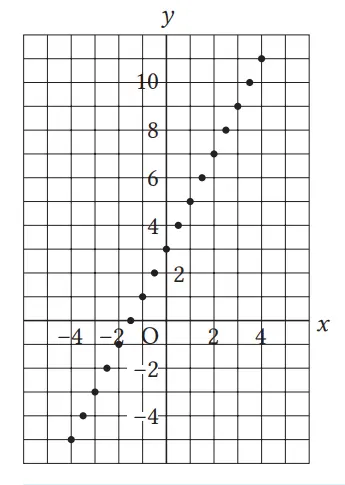
Secara intuitif, peserta didik mungkin memahami bahwa sembilan titik dalam merupakan sejenis, yaitu bilangan bulat. Selanjutnya, peserta didik memprediksi bagaimana titik-titik di antaranya yang belum ada dalam tabel di .

Konfirmasikan bahwa grafik adalah sekumpulan semua titik yang koordinatnya merupakan nilai x dan y yang bersesuaian. Selain itu, perlu juga untuk menyelidiki titik-titik lain, seperti pada Soal 1. Peserta didik yang tidak mengalami masalah, harus mendapatkan lebih banyak titik.

Berdasarkan pembelajaran ini, peserta didik mengamati grafik fungsi linear y = 2x + 3 akan menjadi grafik seperti apa nantinya.

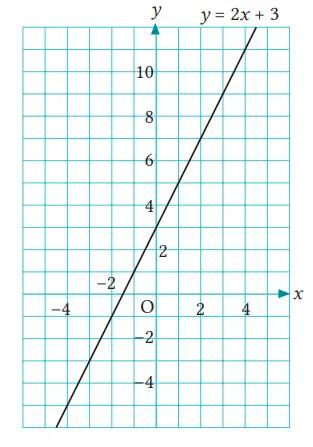
Pada fungsi linear y = 2x + 3, bila kita gambarkan titik-titiknya, maka kumpulan titik-titik tersebut akan menjadi sebuah garis seperti digambarkan di sebelah kanan. Garis ini adalah grafik dari fungsi linear y = 2x + 3.

Berpikir Matematis

Perhatikan bahwa jika banyak sekali titik yang digambarkan, maka himpunan titik tersebut membentuk sebuah garis.

Soal 2

Pada fungsi linear y = –2x + 3, carilah pasangan nilai dari x dan y, kemudian gambarlah grafiknya pada bidang Cartesius.

Jawaban:

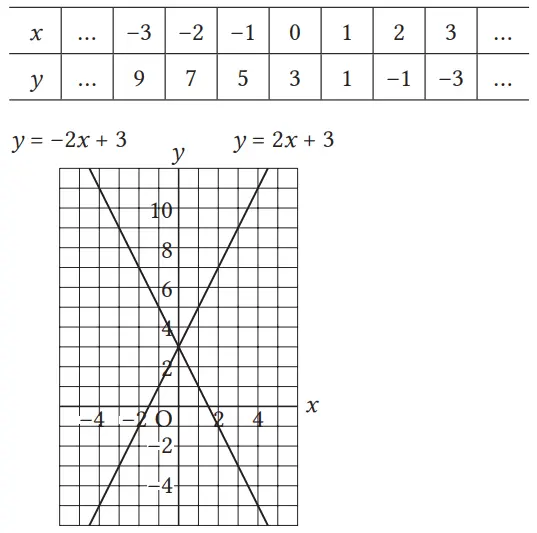
Mari kita selidiki perbedaan antara grafik fungsi linear dan grafik perbandingan senilai.

Q. Lengkapi tabel berikut dan gambarkan grafik dari fungsi linear y = 2x pada bidang Cartesius.

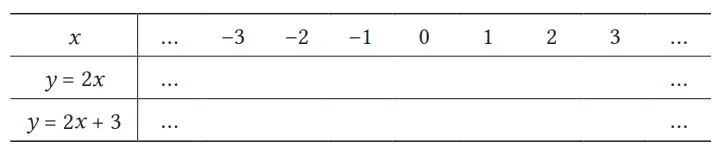
Jawaban:

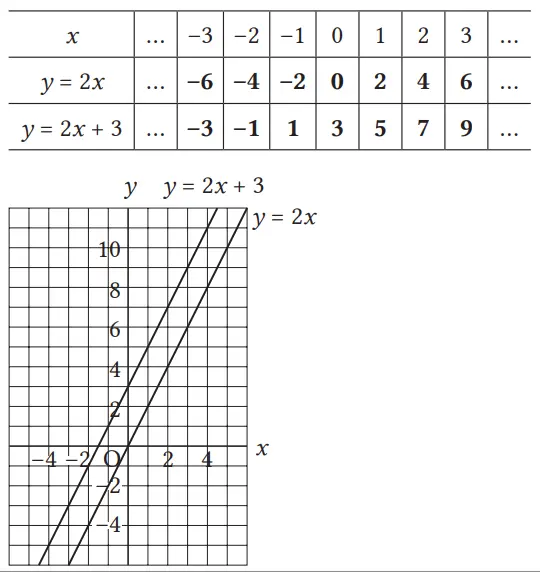
Diketahui bahwa grafik y = 2x + 3 berupa garis, maka dapat dicari hubungannya dengan grafik perbandingan senilai (fungsi linear) y = 2x. Biasanya, dari setiap persamaan, dibuat tabelnya kemudian digambar grafiknya. Akan tetapi, di sini tabel dari kedua persamaan dibuat jadi satu agar lebih mudah membandingkan nilai y. Dari tabel, perhatikan bahwa untuk nilai x yang sama, nilai 2x + 3 selalu lebih besar dari nilai 2x dan selisihnya selalu 3.

Dengan melihat grafik, diharapkan peserta didik menyadari bahwa kedua grafik tersebut sejajar. Disini, jika peserta didik fokus pada titik-titik dengan nilai x yang sama, maka diketahui bahwa titik grafik y = 2x + 3 berada pada posisi di atas titik grafik y = 2x dan bergeser hanya 3 satuan ke arah atas.

Berdasarkan pengamatan tersebut, peserta didik dibuat memahami bahwa grafik y = 2x + 3 adalah garis hasil pergeseran grafik y = 2x sebanyak 3 satuan searah sumbu y positif.

Fungsi linear y = 2x menyatakan hubungan perbandingan senilai. Grafiknya melalui titik pusat koordinat. Juga, untuk setiap nilai x, nilai dari 2x + 3 selalu lebih besar 3 daripada 2x. Oleh karena itu, grafik 2x + 3 adalah berupa garis yang diperoleh dengan cara mentranslasikan atau menggeser grafik y = 2x sejauh 3 satuan searah sumbu y positif.

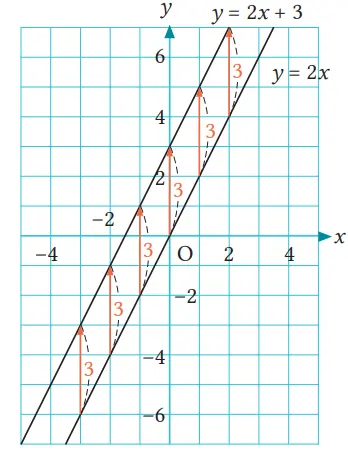
Soal 3

Grafik dari fungsi linear y = 2x – 3 adalah sebuah garis yang diperoleh dengan menggeser grafik y = 2x ke arah mana?

jawaban:

Ke arah sumbu y negatif sebanyak 3 satuan.

Soal 4

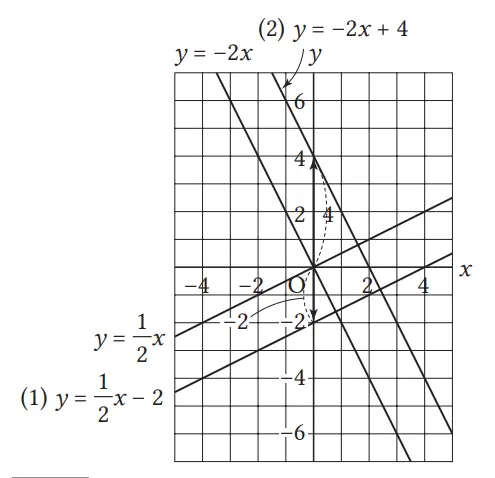
Dengan menggunakan grafik y = 1/2 x atau grafik y = –2x, gambarlah grafik dari fungsi linear berikut

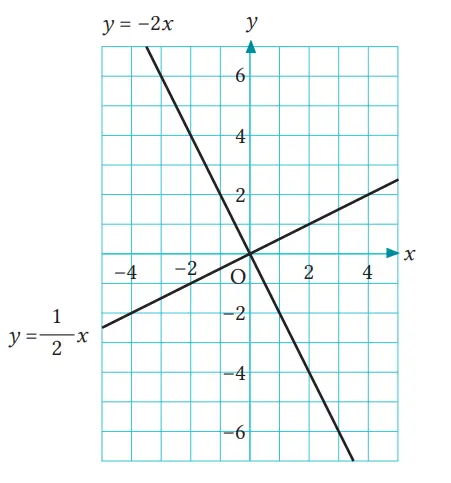
(1) y = 1/2 x – 2

(2) y = –2x + 4

Jawaban:

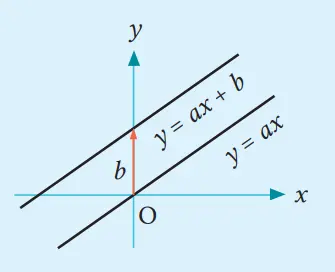
Jika b positif, maka grafik dari fungsi linear y = ax + b adalah sebuah garis yang diperoleh dengan menggeser grafik y = ax sejauh b satuan dan searah sumbu y positif. Bagaimana dengan b negatif?

Konstanta b pada fungsi linear y = ax + b adalah nilai dari y ketika x = 0. Hal ini berarti bahwa b adalah koordinat y dari titik (0, b), yakni ketika grafik y = ax + b memotong sumbu y.

Nilai b inilah yang disebut intersep grafik fungsi linear y = ax + b dengan sumbu y, b juga dinamakan intersep y. Sebagai contoh, intersep dari grafik y = 2x + 3 dengan sumbu y adalah 3.

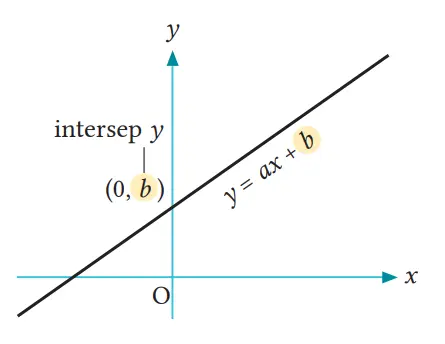
Catatan Intersep y adalah nilai y ketika grafik memotong sumbu y.

Soal 5

Tentukan titik potong dari grafik (1) dan (2) di Soal 4.

(1) –2           (2) 4

Q. Berapakah tingkat perubahan dari fungsi linear y = 2x + 3?

Jawaban:

Tingkat perubahannya 2

Tingkat perubahan dari fungsi linear y = 2x + 3 adalah

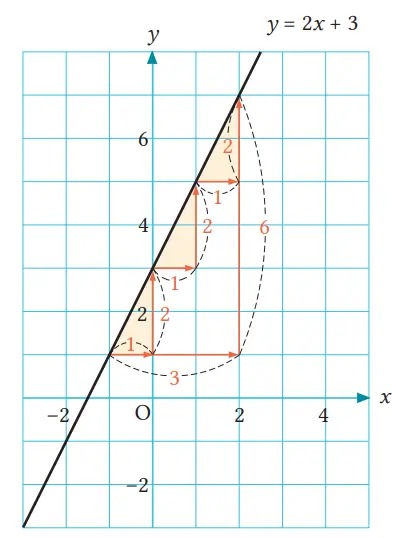
Hal ini berarti, ketika nilai x naik 1, maka nilai y naik 2, dan ketika nilai x naik 3, maka nilai y naik sebanyak 6. Oleh karena itu, jika kita menggeser satu titik pada grafik y = 2x + 3, satu satuan ke kanan dan 2 satuan ke atas, atau 3 satuan ke kanan dan 6 satuan ke atas, maka hasil pergeseran itu akan tetap berada pada grafik.

Soal 6

Gambar di samping kanan merupakan upaya penyelidikan hubungan antara posisi dua titik pada grafik fungsi linear y = –2x + 3. Isilah tiap [] pada gambar tersebut.

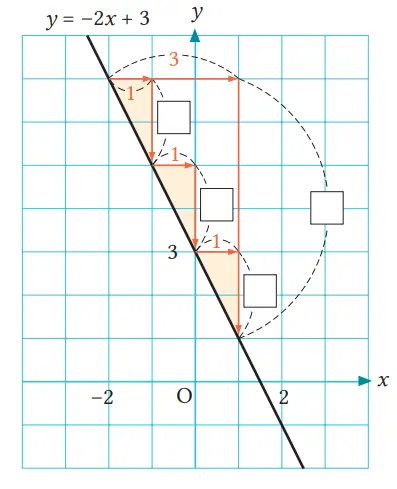
Jawaban:

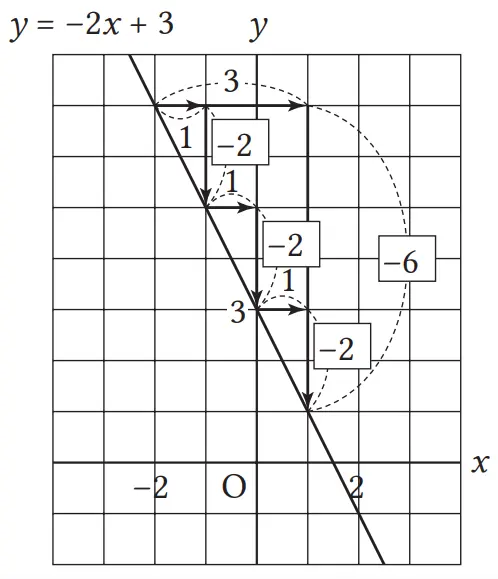
Soal ini untuk mencari pergerakan titik di grafik saat tingkat perubahan bernilai negatif. Agar mudah dipahami, peserta didik ditunjukkan bahwa

–2 = –2/1 = –4/2 = –6/3 …

Nilai y yang negatif, artinya bergeser turun. Peserta didik dapat menyimpulkan bahwa grafiknya adalah garis yang turun ke kanan.

Soal 7

Diskusikan perbedaan grafik-grafik fungsi linear antara yang memiliki tingkat perubahan positif dan yang memiliki tingkat perubahan negatif

Jawaban:

Saat tingkat perubahan fungsi linear nilainya positif, maka grafiknya akan naik ke kanan. Saat tingkat perubahan fungsi linear nilainya negatif, maka grafiknya akan turun ke kanan.

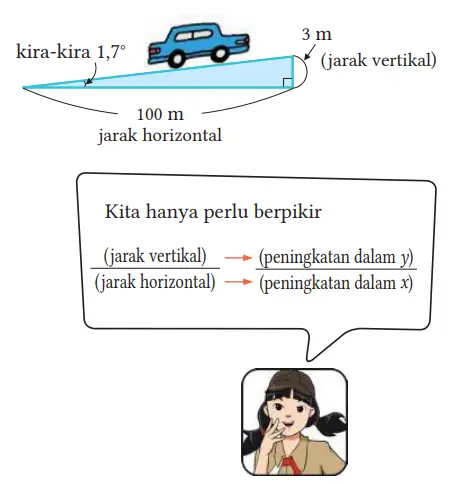
Kemiringan suatu bidang miring atau suatu tangga dapat ditentukan dengan

(Jarak vertikal)/(Jarak horizontal)

Sebagai contoh, kita dapat menggunakan 3/100 untuk menyatakan kemiringan bidang miring seperti gambar di sebelah kanan.

Secara serupa, kemiringan dari sebuah grafik dari fungsi linear y = ax + b bergantung pada tingkat perubahan a. Untuk alasan ini, a disebut kemiringan atau gradien dari grafik fungsi linear. Sebagai contoh, kemiringan dari grafik fungsi linear y = 2x + 3 adalah 2.

Soal 8

Tentukan kemiringan dari tiap grafik fungsi-fungsi linear berikut.

(1) y = 1/2x

(2) y = –2x + 4

Jawaban:

(1) 1/2 (2) –2

Cermati

Kemiringan dari Jalan Landai

Berdasarkan “Peraturan Pengembangan Kota” dari Provinsi Chiba di Jepang, bila membangun jalan landai sebagai tempat umum, maka “kemiringan jalan tidak boleh melebihi seperdua belas”.

Berdasarkan standar tersebut, bila membangun jalan landai dengan kenaikan 50 cm, paling sedikit berapa meterkah jarak horizontal dari jalan tersebut?

Jawaban:

Jika jarak horizontal adalah x m, maka 0,5/x = 1/12, artinya x = 6.

Jawaban: perlu mengambil 6 m atau lebih

Dari yang sudah kita pelajari sejauh ini, grafik fungsi linear dapat dirangkum seperti berikut.

Grafik fungsi linear y = ax + b adalah sebuah garis dengan kemiringan a dan intersep y adalah b.

(1) Jika a > 0, maka grafik naik ke kanan

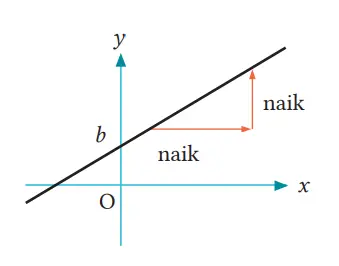
(2) Jika a < 0, maka grafik turun ke kanan

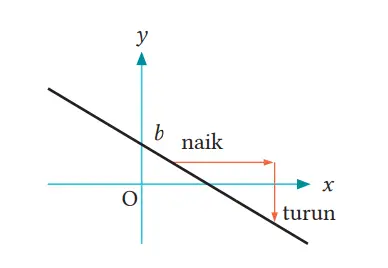
Catatan Semakin besar nilai x atau y, maka dikatakan naik. Semakin kecil nilai x atau y, maka dikatakan turun.

Soal 9

Jika kita menggunakan fungsi y = –2x + 3 untuk menunjukkan hubungan antara tabel, persamaan, dan grafik fungsi linear, maka kita memperoleh gambar berikut. Isilah tiap tanda [] pada gambar berikut.

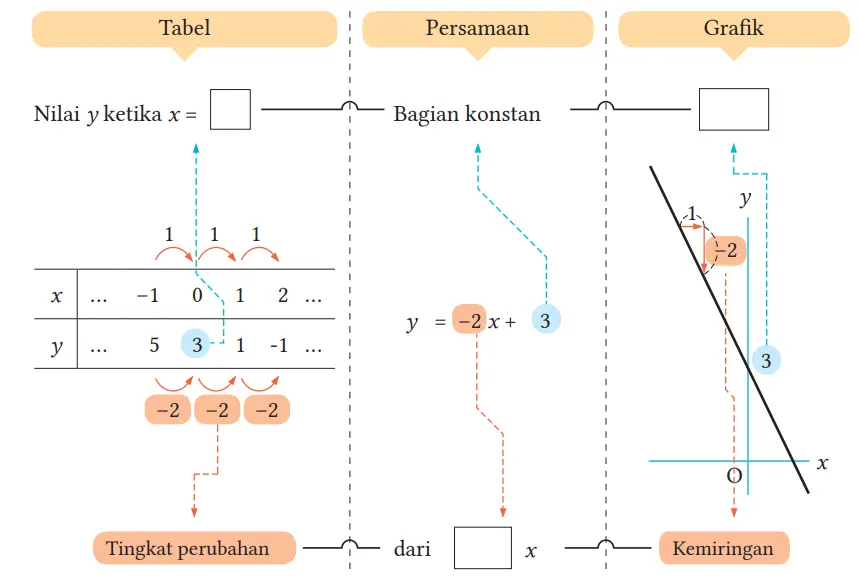
Jawaban:

Berurutan dari kiri: 0, koefisien, intersep y

Peserta didik telah mengamati fungsi linear dengan menggunakan tabel, persamaan, dan grafik. Soal 9 digunakan untuk merangkum hubungan ketiga cara agar peserta didik dapat memahaminya secara satu kesatuan. Mengonfirmasi ulang representasi nilai a dan b pada fungsi linear y = ax + b pada masingmasing tabel dan grafik.

Peserta didik telah mengetahui hubungan fungsi linear dan grafik, maka secara kritis peserta didik diminta apakah bisa membuat grafik dari persamaan atau mencari persamaan dari grafik ini, sehingga dapat berlanjut ke pembelajaran di halaman berikutnya.

Disclaimer:

Kunci jawaban pada unggahan kontenjempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 8 Grafik Fungsi Linear halaman 66 Fungsi Linear. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat mengakses melalui kontenjempolan.id.