kontenjempolan.id-Kunci Jawaban Luas Permukaan Bangun Ruang Halaman 214 Berbagai Cara Mengamati Bangun Ruang Matematika SMP Kelas 7 Kurikulum Merdeka.

Berbagai Cara Mengamati Bangun Ruang

Luas Permukaan Bangun Ruang

Siswa mampu menghitung luas permukaan bangun-bangun ruang.

Luas Permukaan Prisma dan Tabung

Q. Gambar di samping kanan ini merupakan jaring-jaring prisma segitiga. Berdasarkan jaring-jaring tersebut, hitunglah luas permukaan seluruhnya.

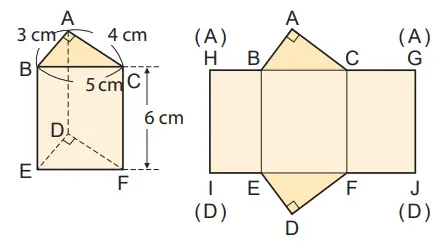
Jawaban:

a. Luas alas = 1/2 × 4 × 3 = 6 (cm²)

b. Luas selimut = 6 × (3 + 4 + 5) = 72 (cm²)

c. Luas permukaan = 72 + 6 × 2 = 84 (cm²)

Luas seluruh permukaan bangun ruang disebut luas permukaan. Selanjutnya Luas dari alas bangun ruang disebut luas alas.  Seterusnya luas seluruh permukaan selimut disebut luas selimut.

1. Pada prisma segitiga di Q , sebutkan manakah yang merupakan alas dan permukaan selimut.

Jawaban:

a. Alas…permukaan ABC, DEF

b. Selimut…permukaan ADEB, BEFC, CFDA

Menghitung luas permukaan tabung dan prisma adalah Luas permukaan sama dengan dua kali luas alas + luas selimut

2. Pada tabung berikut ini, hitunglah luas alas, luas selimut, dan luas permukaannya. Nilai pendekatan untuk π adalah 3,14.

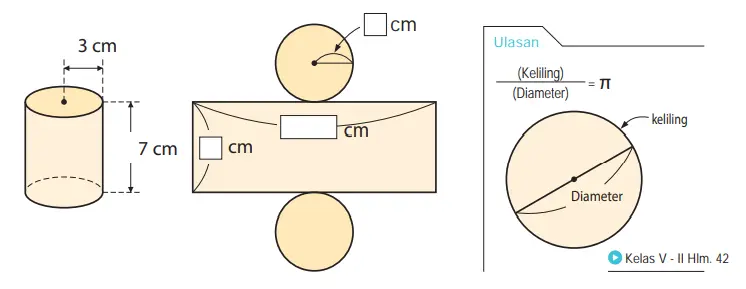
Jawaban:

a. Luas alas = 3 × 3 × 3,14 = 28,26 (cm²)

b. Luas selimut = 7 × (3 × 2 × 3,14) = 131,88 (cm²)

c. Luas permukaan = 131,88 + 28,26 × 2 = 188,4 (cm²)

Rasio keliling terhadap garis tengah lingkaran menghasilkan satu nilai, yaitu 3,14159265389793238462643383279…, bilangan ini berlanjut tak terhingga, dan dinyatakan dalam huruf Yunani π.

Contoh 1

Pada lingkaran berjari-jari r cm, kelilingnya adalah K cm, dan luasnya adalah L cm2

(Keliling)
= (garis tengah) × π
= (r × 2) × π = 2πr

(Luas lingkaran)
= (jari-jari) × (jari-jari) × π
= r × r × π =πr²

π berbeda dengan huruf dalam bentuk aljabar dan persamaan yang telah kita pelajari sebelumnya. π menyajikan bilangan tertentu. Oleh karena itu, dalam perkalian kita tulis setelah bilangan dan sebelum huruf.

Rumus Lingkaran

Keliling Lingkaran

K = 2πr

Luas Lingkaran

L = πr²

catatan : r, K, dan L adalah huruf pertama dari radius (jari-jari), keliling, luas lingkaran.

3. Hitunglah panjang keliling dan luas lingkaran yang berjari-jari 7 cm.

Jawaban:

Jika panjang keliling adalah l cm, luas adalah S cm², maka

K = 2π × 7
= 14π (cm)

Jadi l = 14 x 22/7 = 44

L = π × 7²
= 49π (cm2)

Jadi S= 49 x 22/7 = 154

4. Hitunglah luas permukaan bangun ruang berikut ini.

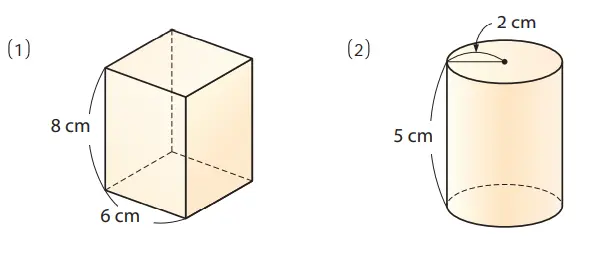
Jawaban:

(1) a. Luas alas = 6 × 6 = 36 (cm²)

b. Luas selimut = (6 × 8) × 4 = 192 (cm²)

c. Luas permukaan = 192 + 36 × 2 = 264 (cm²)

(2) a. Luas alas = π × 22 = 4π (cm²)
= 4 x 3.14 = 12,56 cm2

b. Luas selimut = (2π × 2) × 5 = 20π (cm²)
= 20 x 3.14 = 62,8 cm2

c. Luas permukaan = 20π + 4π × 2 = 28π (cm²)
= 28x 22/7 = 88 cm²

Luas Permukaan Limas

Contoh 2

Hitunglah luas permukaan limas persegi yang ditunjukkan di samping kanan ini.

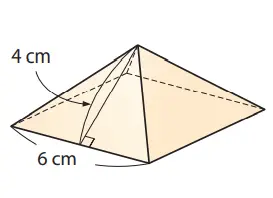
Jawaban:

Caranya Hitung luas alas dan luas selimut, kemudian jumlahkan.

Penyelesaian

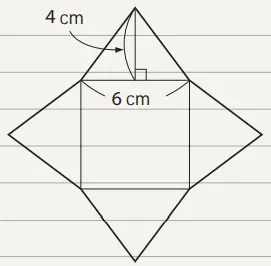
Bentuk alas adalah persegi dengan panjang rusuk 6 cm,

6 × 6 = 36

Jadi, luas alas adalah 36 cm².

Permukaan miring berupa segitiga sama kaki dengan alas 6 cm, dan tinggi 4 cm, sehingga luas selimut adalah

1/2 × 6 × 4 × 4 = 48

Jadi, luas selimut adalah 48 cm².

36 + 48 = 84

Jawab: 84 cm²

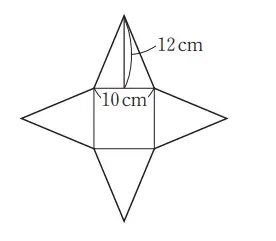
5. Hitunglah luas alas, luas selimut, dan luas permukaan limas di samping ini.

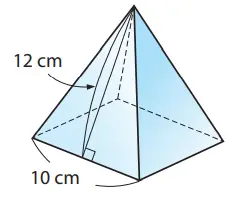
Jawaban:

a. Luas alas = 10 × 10 = 100 (cm²)

b. Luas selimut = (1/2 x 10 x 12) x 4 = 240 (cm²)

c. Luas permukaan = 240 + 100 = 340 (cm²)

Luas Permukaan Kerucut

Q. Apa yang perlu kita ketahui agar dapat menghitung luas permukaan kerucut berikut ini?

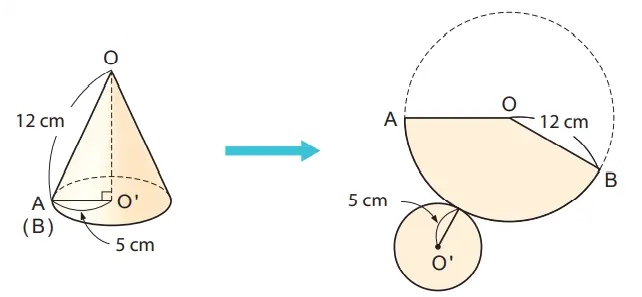
Jawaban:

Yang perlu diketahui hanyalah luas juring selimutnya. Oleh karena itu, perlu dicari panjang busur dan besar sudut pusatnya.

Marilah kita cermati luas juring untuk menghitung luas permukaan kerucut.

Pada lingkaran, panjang tali busur juring berbanding lurus dengan ukuran sudut dalam. Luas juring berbanding lurus dengan ukuran sudut dalam.

6. Pada lingkaran, apakah kita dapat menyimpulkan bahwa luas juring berbanding lurus dengan panjang tali busur juring tersebut?

Jawaban:

Jika panjang tali busur menjasi 2 kali lipat, 3 kali lipat…dst, maka luas pun akan menjadi 2 kali lipat, 3 kali lipat…dst. oleh karenanya, dapat dikatakan bahwa luas permukaan juring berbanding lurus dengan panjang tali busurnya.

7. Untuk juring dengan jari-jari 6 cm dan sudut dalam 120º, jawablah pertanyaan berikut ini.

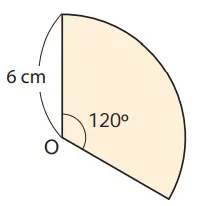
(1) Jika juring dan lingkaran mempunyai jari-jari yang sama, berapa kali luas juring lingkaran sama dengan luas lingkaran?

Jawaban:

120/360 = 1/3, maka 1/3 kali lipat

(2) Hitung luas juring.

Jawaban:

π × 62 × 1/3 = 12π (cm²)

(3) Hitung panjang tali busur

Jawaban:

2π × 6 × 1/3 = 4π (cm)

Panjang Tali Busur dan Luas Juring

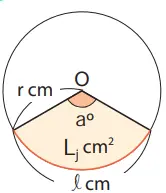
Diberikan juring dengan jari-jari r cm dan sudut dalam aº. Panjang tali busur adalah l cm dan luas juring adalah Lj cm2,

l = 2πr × a/360, Lj = πr2 x a/360

8. Hitunglah panjang tali busur dan luas juring dengan jari-jari 4 cm dan sudut dalam 135º.

Jawaban:

Jika panjang tali busur juring adalah l cm, dan luas adalah S cm2, maka

l = 2π × 4 ×135/360 = 3π (cm)

L = π × 42 × 135/360 = 6π (cm²)

 

Disclaimer:

Kunci jawaban pada unggahan kontenjempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 7 SMP halaman 214 Luas Permukaan Bangun Ruang, Berbagai Cara Mengamati Bangun Ruang. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat diakses melalui kontenjempolan.id.