kontenjempolan.id-Kunci Jawaban Latihan 6.3 Halaman 159 Menentukan Fungsi Kuadrat dan Titik Maksimum/Titik Minimum Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.

Latihan 6.3

1. Tentukan berapa banyaknya titik potong dari fungsi kuadrat berikut.

a. f(x)= 3x² + 4x + 1

b. f(x)= -4x² + 4x + 5

c. f(x)= -3x² + 4x + 1

d. f(x)= 4x² + 4x + 5

e. f(x)= x² + 2x + 1

f. f(x)= -2x² + 3x + 5

g. f(x)= -3x² + 8x – 1

h. f(x)= 4x² + 11x – 7

Jawaban:

a. dua

b. dua

c. dua

d. Tidak ada

e. satu

f. dua

g. dua

h. dua

2. Tentukan koordinat titik puncak, sumbu simetri, koordinat titik potong dengan sumbu y, dan banyak titik potong dari grafik fungsi-fungsi kuadrat di bawah ini.

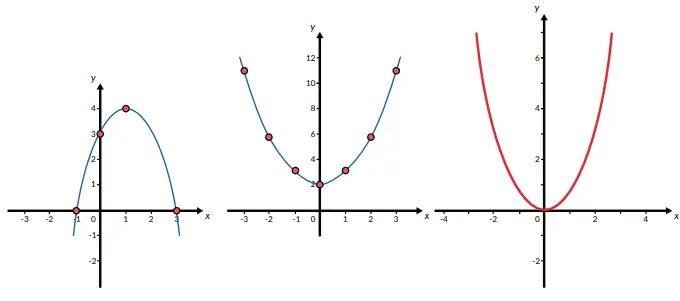
Apakah hubungan antara titik puncak dengan grafik terbuka ke atas atau ke bawah?

Jawaban:

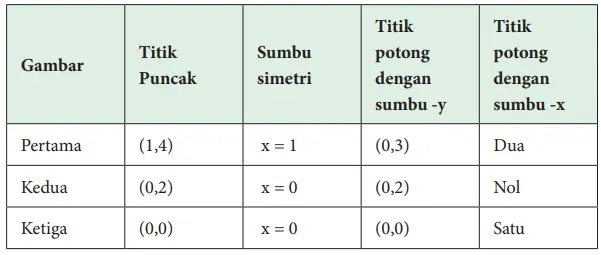
a. Titik maksimum terjadi jika grafik terbuka ke bawah.
b. Titik minimum terjadi jika grafik terbuka ke atas.

3. Perhatikan tabel di bawah ini, yang menunjukkan jarak tempuh suatu mobil sebagai fungsi dari waktu

a. Berapa jarak maksimum yang ditempuh?

Jawaban:

Jarak maksimum adalah 17 m.

b. Berapa koordinat titik maksimum?

Jawaban:

Koordinat titik maksimum (3,17).

c. Tentukan persamaan garis sumbu simetri.

Jawaban:

Sumbu simetri x = 3.

4. Perhatikan tabel di bawah ini, yang menunjukkan biaya produksi sebagai fungsi dari jumlah barang.

a. Berapa biaya minimum?

Jawaban:

Biaya minimum adalah 400.

b. Berapa koordinat titik minimum?

Jawaban:

Koordinat titik minimum adalah (20,400).

c. Tentukan persamaan garis sumbu simetri.

Jawaban:

Sumbu simetri x = 20

Ayo Berpikir Kritis

5. Untuk setiap kasus di bawah ini tentukan apakah grafik fungsi kuadrat terbuka ke atas atau ke bawah.

a. Biaya produksi sebagai fungsi dari jumlah barang.

Jawaban:

Biaya minimum maka grafik terbuka ke atas.

b. Keuntungan sebagai fungsi dari jumlah barang.

Jawaban:

Keuntungan maksimum maka grafik terbuka ke bawah.

c. Kualitas bunyi dari sound system sebagai fungsi dari amplitudo gelombang bunyi.

Jawaban:

Kualitas bunyi maksimum maka grafik terbuka ke bawah.

d. Efektivitas obat sebagai fungsi dari dosis obat.

Jawaban:

Efektivitas maksimum maka grafik terbuka ke bawah.

e. Keselamatan pemakaian suatu bahan sebagai fungsi dari waktu pemakaian.

Jawaban:

Keselamatan maksimum maka grafik terbuka ke bawah.

Disclaimer:

Kunci jawaban pada unggahan kontenjempolan tidak mutlak kebenarannya dan unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

Demikian pembahasan Matematika Kelas 10 SMA/SMK halaman 155 Eksplorasi 6.5, Menentukan Titik Maksimum, Titik Minimum dan Sumbu Simetri. Untuk mendapatkan pembahasan Soal latihan Kurikulum Merdeka Mata Pelajaran lainnya dapat diakses melalui kontenjempolan.id.